
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

科目:初中数学 来源: 题型:
【题目】如图,把一张长是a,宽是b的长方形硬纸板的四周各剪去一个边长为c的正方形(a>b>2c).再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)若a=12,b=7,c=2,求折合成的长方体盒子的侧面积是多少?
(2)请用含a,b,c的代数式表示折成的长方体盒子的底面周长;
(3)如果把长方体硬纸板的四周剪去2个边长为c的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的底面周长是多少?(用含a,b,c的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类讨论是一种重要的数学方法,如在化简|a|时,可以这样分类:当a>0时,|a|=a;当a=0时,|a|=0;当a<0时,|a|=﹣a.用这种方法解决下列问题:
(1)当a=5时,求![]() 的值.
的值.
(2)当a=﹣2时,求![]() 的值.
的值.
(3)若有理数a不等于零,求![]() 的值.
的值.
(4)若有理数a、b均不等于零,试求![]() +
+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
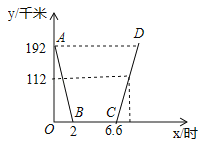
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为285元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六.星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) | +7 | +5 |
|
| +8 |
问:(1)本周星期三黄金的收盘价是多少?
(2)本周黄金收盘时的最高价.最低价分别是多少?
(3)上周,小王以周五的收盘价285元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
![]() 若汽车耗油量为
若汽车耗油量为![]() 升/千米,则当天耗油多少升?若汽油价格为
升/千米,则当天耗油多少升?若汽油价格为![]() 元/升,则小王共花费了多少元钱?
元/升,则小王共花费了多少元钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com