
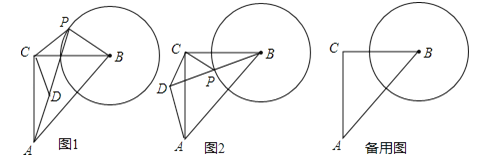
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC=![]() ,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为 ;
(3)如图2,当B、P、D三点在同一条直线上时,求BD的长;
(4)BD的最小值为 ;BD的最大值为 .
【答案】(1)答案见解析;(2)∠CPB=45°或135°;(3)![]() ;(4)1,3.
;(4)1,3.
【解析】分析: (1)根据SAS即可证明△ACD≌△BCP,再根据全等三角形的性质可得AD=BP;
(2)利用切线的性质结合等腰直角三角形得出即可;
(3)当B、P、D三点在同一条直线上时利用勾股定理,可得BD的长;
(4)当∠PBC=45°时,BD有最小值;进而得出BD有最大值.
详解: (1)证明:如图1,
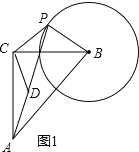
∵∠ACB=90°,∠DCP=90°,
∴∠ACD=∠BCP
在△ACD与△BCP中,
∵
AC=BC
∠ACD=∠BCP
CD=CP
∴△ACD≌△BCP(SAS)
∴AD=BP;
(2)解:如图2,
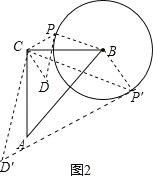
∵CP=CD,DP是⊙B的切线,∠PCD=90°,
∴∠BPD=90°,∠ADP=∠APD=45°,
∴∠CPB=45°+90°=135°,
同理可得:∠CPB=45°
故∠CPB=45°或135°;
故答案为:故∠CPB=45°或135°;
(3)解:∵△CDP为等腰直角三角形,
∴∠CDP=∠CPD=45°,∠CPB=135°,
由(1)知,△ACD≌△BCP,
∴∠CDA=∠CPB=135°,AD=BP=1,
∴∠BDA=∠CDA∠CDP=90°,
在Rt△ABC中,AB=![]() =2,
=2,
∴BD=![]() =
=![]() ;
;
(4)解:如图3,
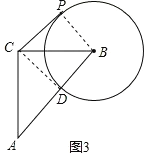
当B、D、A三点在同一条直线上时,BD有最小值,
由(1)得△ACD≌△BCP,
此时∠PBC=45°时,BD的最小值为1;
同理可得:如图4,
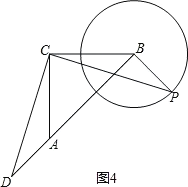
当B、D、A三点在同一条直线上时,
由(1)得△ACD≌△BCP,BD的最大值为:AB+AD=AB+BP=3.
故答案为:1,3.
点睛: 此题考查了圆的综合题,涉及的知识有全等三角形的判定与性质,分类思想的运用,最大值与最小值,注意分析问题要全面,以免漏解,有一定的难度.


科目:初中数学 来源: 题型:
【题目】计算
(1)8÷(﹣2)2﹣4×(﹣3)﹣|﹣6|
(2)(![]() )×(﹣12)
)×(﹣12)
(3)(4x+2y)-3(x-2y)
(4)4ab2-3[a2b-2(a2b-2ab2)]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
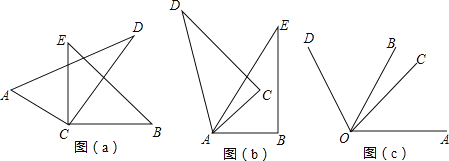
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
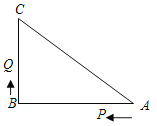
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨实验学校为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买1副围棋和1副中国象棋需用26元;若购买8副围棋和3副中国象棋需用158元;
(1)求每副围棋和每副中国象棋各多少元;
(2)实验中学决定购买围棋和中国象棋共40副,总费用550元,那么实验中学可以购买多少副围棋.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
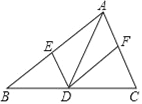
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
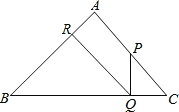
【题目】如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.
(1)求证:PQ=CQ;
(2)设CP的长为x,QR的长为y,求y与x之间的函数关系式及自变量x的取值范围,并在平面直角坐标系作出函数图象.
(3)PR能否平行于BC?如果能,试求出x的值;若不能,请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,t= ;
(2)当t=4时,直接写出S的值;
(3)求出S与t的函数关系式;
(4)若S=12,则t= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com