
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
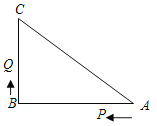
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间;
【答案】(1)PQ=2![]() ;(2)t=
;(2)t=![]() ;(3)t=5.5,t=6,t=6.6秒时,△BCQ为等腰三角形.
;(3)t=5.5,t=6,t=6.6秒时,△BCQ为等腰三角形.
【解析】
(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)由题意得出BQ=BP,即2t=8-t,解方程即可;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时(图1),则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时(图2),则BC+CQ=12,易求得t;
③当BC=BQ时(图3),过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
解:(1)∵∠B=90°,AB=8cm,BC=6cm,
根据勾股定理可得:AC=10
∴BQ=2×2=4cm,BP=AB-AP=8-2×1=6cm,
∵∠B=90°,
PQ=![]() (cm);
(cm);
(2)解:根据题意得:BQ=BP,
即2t=8-t,
解得:t=![]() ;
;
即出发时间为:![]() 秒时,△PQB是等腰三角形;
秒时,△PQB是等腰三角形;
(3)解:分三种情况:
①当CQ=BQ时,如图1所示:
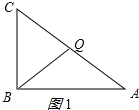
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
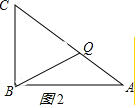
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
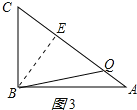
过B点作BE⊥AC于点E,
则BE=![]() =
=![]() =4.8(cm)
=4.8(cm)
∴CE=![]() =3.6cm,
=3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“方便交通,绿色出行”,人们常选择以共享单车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.
(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)
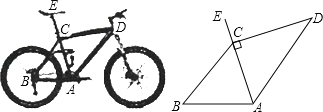
图(1) 图(2)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,……排成如下表:如图所示,图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数.
1 | 3 | 5 | 7 | 9 |
11 | 13 | 15 | 17 | 19 |
21 | 23 | 25 | 27 | 29 |
31 | 33 | 35 | 37 | 39 |
… | … | … | … | … |
(1)设T字框内处于中间且靠上方的数是整个数表当中从小到大排列的第n个数,请你用含n的代数式表示T字框中的四个数的和;
(2)若将T字框上下左右移动,框住的四个数的和能等于2020吗?如能,写出这四个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形![]() 的边长是1米;
的边长是1米;
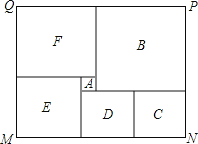
(1)若设图中最大正方形![]() 的边长是
的边长是![]() 米,请用含
米,请用含![]() 的代数式分别表示出正方形
的代数式分别表示出正方形![]() 的边长
的边长
(2)观察图形的特点可知,长方形相对的两边是相等的(即![]() ,
, ![]() )请根据以上结论,求出
)请根据以上结论,求出![]() 的值
的值
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
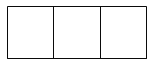
【题目】(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;
(2)若在如图三个空格的右侧增加一个空格,将A、B、C、D四个字母任意填写其中(每空填一个字母,每空中的字母不重复),从左往右字母顺序恰好是A、B、C、D的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
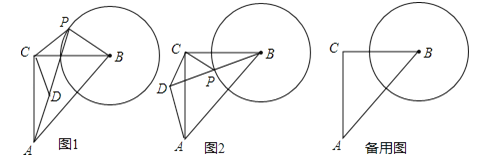
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC=![]() ,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为 ;
(3)如图2,当B、P、D三点在同一条直线上时,求BD的长;
(4)BD的最小值为 ;BD的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴正半轴上的![]() ,
,![]() 两点分别表示有理数
两点分别表示有理数![]() ,
,![]() ,
,![]() 为原点,若
为原点,若![]() ,线段
,线段![]() .
.

(1)![]() ______,
______,![]() ______;
______;
(2)若点![]() 从点
从点![]() 出发,以每秒2个单位长度向
出发,以每秒2个单位长度向![]() 轴正半轴运动,求运动时间为多少时;点
轴正半轴运动,求运动时间为多少时;点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 距离的3倍;
距离的3倍;
(3)数轴上还有一点![]() 表示的数为32,若点
表示的数为32,若点![]() 和点
和点![]() 同时从点
同时从点![]() 和点
和点![]() 出发,分别以每秒2个单位长度和每秒1个单位长度的速度向
出发,分别以每秒2个单位长度和每秒1个单位长度的速度向![]() 点运动,
点运动,![]() 点到达
点到达![]() 点后,再立刻以同样的速度返回,运动到终点
点后,再立刻以同样的速度返回,运动到终点![]() ,求点
,求点![]() 和点
和点![]() 运动多少秒时,
运动多少秒时,![]() 、
、![]() 两点之间的距离为4.
两点之间的距离为4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
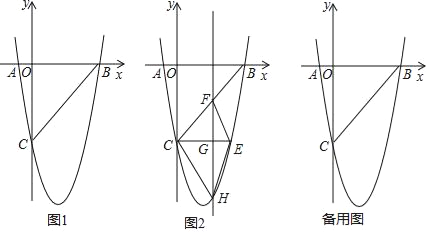
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com