
【题目】阅读材料:若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 也在抛物线
也在抛物线![]() 上(点
上(点![]() 与点
与点![]() 不重合),我们称这样的两条抛物线
不重合),我们称这样的两条抛物线![]() 、
、![]() 互为“友好”抛物线,如图1.
互为“友好”抛物线,如图1.
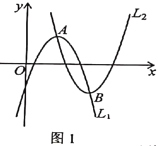
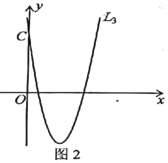
解决问题:如图2,已知物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称,求点
的对称轴对称,求点![]() 的坐标;
的坐标;
(2)求出以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式;
的解析式;
(3)直接写出![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
【答案】(1)点D坐标为(4,4)
(2)抛物线![]() 的解析式为
的解析式为![]()
(3)![]()
【解析】
(1)根据抛物线![]() 的解析式可求得C点坐标及对称轴,即可求得点D坐标.
的解析式可求得C点坐标及对称轴,即可求得点D坐标.
(2)可设![]() 的交点式解析式,将顶点坐标代入即可求解.
的交点式解析式,将顶点坐标代入即可求解.
(3)画图像,根据图像可得![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
解:(1)∵点C是![]() 与
与![]() 轴交点
轴交点
∴点C坐标为(0,4)
将![]() 化成顶点式得:
化成顶点式得:![]()
∴顶点坐标为(2,-4),对称轴为![]()
∵点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称
的对称轴对称
∴点D坐标为(4,4).
(2)设![]() 解析式为:
解析式为:![]()
将(2,-4)代入解得![]()
∴![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式为
的解析式为![]() .
.
(3)画出![]() 的图像.
的图像.

由图像可知当![]() 时,
时,![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大.
增大而增大.
故答案为:(1)点D坐标为(4,4)
(2)抛物线![]() 的解析式为
的解析式为![]()
(3)![]()


科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一动点(与点
边上一动点(与点![]() 不重合),连接
不重合),连接![]() 将
将![]() 的两边所在射线
的两边所在射线![]() 以点
以点![]() 为中心,顺时针旋转
为中心,顺时针旋转![]() 分别交射线
分别交射线![]() 于点
于点![]() .
.
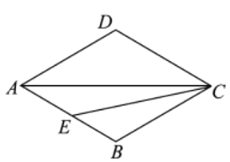
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
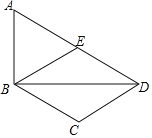
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
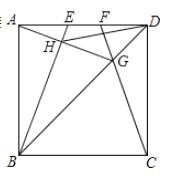
【题目】如图,在边长为4的正方形![]() 中,
中,![]() 是
是![]() 边上的两个动点,且
边上的两个动点,且![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;⑤线段
;⑤线段![]() 的最小值是
的最小值是![]() .正确的个数有( )
.正确的个数有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市要进一批鸡蛋进行销售,有![]() 、
、![]() 两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
(1)下列抽样方式比较合理的是哪一种?请简述原因.
①分别从![]() 、
、![]() 两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
②分别从![]() 、
、![]() 两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
(2)在用合理的方法抽出两家提供的鸡蛋各40枚后,分别称出每个鸡蛋的质量(单位:![]() ),结果如表所示(数据包括左端点不包括右端点).
),结果如表所示(数据包括左端点不包括右端点).
45~47 | 47~49 | 49~51 | 51~53 | 53~55 | |
| 2 | 8 | 15 | 10 | 5 |
| 4 | 6 | 12 | 14 | 4 |
①如果从这两家农场提供的鸡蛋中随机拿一个,分别估计两家鸡蛋质量在![]() (单位:
(单位:![]() )范围内的概率(数据包括左端点不包括右端点);
)范围内的概率(数据包括左端点不包括右端点);
②如果你是超市经营者,试通过数据分析确定选择哪家农场提供的鸡蛋.
查看答案和解析>>
科目:初中数学 来源: 题型:
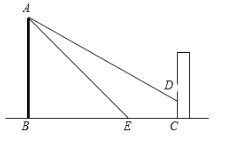
【题目】如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)
参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ),经过点
),经过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(Ⅰ)求抛物线的解析式;
(Ⅱ)若点![]() 是射线
是射线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,交抛物线于点
,交抛物线于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,已知
,已知![]() ,
,![]() 是以
是以![]() 为未知数的一元二次方程
为未知数的一元二次方程![]() (
(![]() 为常数)的两个实数根,点
为常数)的两个实数根,点![]() 在抛物线上,连接
在抛物线上,连接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,求出
,求出![]() 值及点
值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com