
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЪЧГЃЪ§ЃЌЧв
ЪЧГЃЪ§ЃЌЧв![]() ЃЉЃЌОЙ§Еу
ЃЉЃЌОЙ§Еу![]() ЃЌ
ЃЌ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
ЃЈЂёЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈЂђЃЉШєЕу![]() ЪЧЩфЯп
ЪЧЩфЯп![]() ЩЯвЛЕуЃЌЙ§Еу
ЩЯвЛЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌДЙзуЮЊЕу
жсЕФДЙЯпЃЌДЙзуЮЊЕу![]() ЃЌНЛХзЮяЯпгкЕу
ЃЌНЛХзЮяЯпгкЕу![]() ЃЌЩш
ЃЌЩш![]() ЕуКсзјБъЮЊ
ЕуКсзјБъЮЊ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉдкЃЈЂђЃЉЕФЬѕМўЯТЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌЩш
ЩЯЪБЃЌЩш![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЪЧвд
ЪЧвд![]() ЮЊЮДжЊЪ§ЕФвЛдЊЖўДЮЗНГЬ
ЮЊЮДжЊЪ§ЕФвЛдЊЖўДЮЗНГЬ![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉЕФСНИіЪЕЪ§ИљЃЌЕу
ЮЊГЃЪ§ЃЉЕФСНИіЪЕЪ§ИљЃЌЕу![]() дкХзЮяЯпЩЯЃЌСЌНг
дкХзЮяЯпЩЯЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЦНЗж
ЦНЗж![]() ЃЌЧѓГі
ЃЌЧѓГі![]() жЕМАЕу
жЕМАЕу![]() ЕФзјБъ.
ЕФзјБъ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЛЃЈЂђЃЉ
ЃЛЃЈЂђЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈЂѓЃЉ
ЃЛЃЈЂѓЃЉ![]() жЕЮЊ
жЕЮЊ![]() ЃЌ
ЃЌ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈЂёЃЉНЋЕуA![]() КЭЕуBЃЈ3ЃЌ0ЃЉзјБъДњШыy=a
КЭЕуBЃЈ3ЃЌ0ЃЉзјБъДњШыy=a![]() +bx+3ЕУЕНaКЭbЕФЗНГЬзщЃЌШЛКѓНтЗНГЬЧѓГіaКЭbЃЌМДПЩЕУЕНХзЮяЯпЕФНтЮіЪНЃЛ
+bx+3ЕУЕНaКЭbЕФЗНГЬзщЃЌШЛКѓНтЗНГЬЧѓГіaКЭbЃЌМДПЩЕУЕНХзЮяЯпЕФНтЮіЪНЃЛ
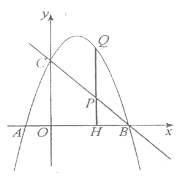
ЃЈЂђЃЉЯШИљОнД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBCЕФНтЮіЪНЃЌЗжЕБЕуPдкЯпЖЮCBЩЯЪБЃЌКЭЕуPдкЩфЯпBNЩЯЪБЃЌСНжжЧщПіЬжТлЃЌ![]() ЕуЕФКсзјБъЮЊ
ЕуЕФКсзјБъЮЊ![]() ЃЌЕУГіPЕуЕФзјБъЮЊЃЈtЃЌ-t+3ЃЉЃЌQЕуЕФзјБъЮЊЃЈtЃЌ-t2+2t+3ЃЉЃЌОЭПЩвдЕУГіdгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЖјЕУГіНсТлЃЛ
ЃЌЕУГіPЕуЕФзјБъЮЊЃЈtЃЌ-t+3ЃЉЃЌQЕуЕФзјБъЮЊЃЈtЃЌ-t2+2t+3ЃЉЃЌОЭПЩвдЕУГіdгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЖјЕУГіНсТлЃЛ
ЃЈЂѓЃЉИљОнИљЕФХаБ№ЪНОЭПЩвдЧѓГіmЕФжЕЃЌОЭПЩвдЧѓГіЗНГЬЕФНтЖјЧѓЕУPQКЭPHЕФжЕЃЌбгГЄMPжСLЃЌЪЙLP=MPЃЌСЌНгLQЁЂLHЃЌбгГЄMPжСLЃЌЪЙLP=MPЃЌСЌНгLQЁЂLHЃЌОЭПЩвдЕУГіЫФБпаЮLQMHЪЧЦНааЫФБпаЮЃЌНјЖјЕУГіЫФБпаЮLQMHЪЧСтаЮЃЌгЩСтаЮЕФаджЪОЭПЩвдЧѓГіНсТлЃЎ
НтЃКЃЈЂёЃЉНЋ![]() ДњШы
ДњШы![]() ЃЌ
ЃЌ
ЕУ![]() НтЕУ
НтЕУ![]()
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЁп![]() ЕуЕФзјБъЮЊ
ЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЩшжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌ
ЃЌ
НЋ![]() ДњШыЃЌЕУ
ДњШыЃЌЕУ![]() .
.
НтЕУ![]() .
.
ЁржБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() .
.
Ёп![]() ЕуЕФКсзјБъЮЊ
ЕуЕФКсзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() ДЙжБгк
ДЙжБгк![]() жсЃЌ
жсЃЌ
Ёр![]() ЕуЕФзјБъЮЊ
ЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕуЕФзјБъЮЊ
ЕуЕФзјБъЮЊ![]() .
.
ЂйШчЭМЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ
![]() .
.
ЂкШчЭМЃЌЕБЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ

![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр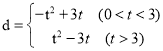
ЃЈЂѓЃЉЁп![]() ЪЧ
ЪЧ![]() ЕФСНИіЪЕЪ§Иљ.
ЕФСНИіЪЕЪ§Иљ.
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
ећРэЕУЃК![]() .
.
Ёр![]() .
.
Ёр![]() .
.
ЁрЗНГЬЮЊ![]() .
.
НтЕУ![]() .
.
Ёп![]() гы
гы![]() ЪЧ
ЪЧ![]() ЕФСНИіЪЕЪ§ИљЃЌ
ЕФСНИіЪЕЪ§ИљЃЌ
Ыљвд![]() .
.
МД![]() .
.
Ёр![]() .
.
ШчЭМЃЌбгГЄ![]() жС
жС![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЪЧЦНааЫФБпаЮ.
ЪЧЦНааЫФБпаЮ.
Ёр![]() .
.
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
Ёр![]() ЪЧСтаЮ.
ЪЧСтаЮ.
Ёр![]() .
.
ЁрЕу![]() ЕФзнзјБъгыЕу
ЕФзнзјБъгыЕу![]() знзјБъЯрЕШЃЌЖМЪЧ
знзјБъЯрЕШЃЌЖМЪЧ![]() .
.
дк![]() жаЃЌЕБ
жаЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .
.
Ёр![]() .
.
НтЕУ![]() .
.
злЩЯЫљЪіЃК![]() жЕЮЊ
жЕЮЊ![]() ЃЌ
ЃЌ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() Лђ
Лђ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§yЃН2x+bЕФЭМЯѓгыxжсЕФНЛЕуЮЊAЃЈ2ЃЌ0ЃЉЃЌгыyжсЕФНЛЕуЮЊBЃЌжБЯпABгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкЕуCЃЈЉ1ЃЌmЃЉЃЎ
ЕФЭМЯѓНЛгкЕуCЃЈЉ1ЃЌmЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉжБНгаДГіЙигкxЕФВЛЕШЪН2x+bЃО![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉЕуPЪЧетИіЗДБШР§КЏЪ§ЭМЯѓЩЯЕФЕуЃЌЙ§ЕуPзїPMЁЭxжсЃЌДЙзуЮЊЕуMЃЌСЌНгOPЃЌBMЃЌЕБSЁїABMЃН2SЁїOMPЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃКШєХзЮяЯп![]() ЕФЖЅЕу
ЕФЖЅЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌХзЮяЯп
ЩЯЃЌХзЮяЯп![]() ЕФЖЅЕу
ЕФЖЅЕу![]() вВдкХзЮяЯп
вВдкХзЮяЯп![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() гыЕу
гыЕу![]() ВЛжиКЯЃЉЃЌЮвУЧГЦетбљЕФСНЬѕХзЮяЯп
ВЛжиКЯЃЉЃЌЮвУЧГЦетбљЕФСНЬѕХзЮяЯп![]() ЁЂ
ЁЂ![]() ЛЅЮЊЁАгбКУЁБХзЮяЯпЃЌШчЭМ1ЃЎ
ЛЅЮЊЁАгбКУЁБХзЮяЯпЃЌШчЭМ1ЃЎ
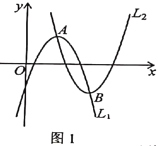
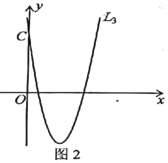
НтОіЮЪЬтЃКШчЭМ2ЃЌвбжЊЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєЕу![]() гыЕу
гыЕу![]() ЙигкХзЮяЯп
ЙигкХзЮяЯп![]() ЕФЖдГЦжсЖдГЦЃЌЧѓЕу
ЕФЖдГЦжсЖдГЦЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓГівдЕу![]() ЮЊЖЅЕуЕФ
ЮЊЖЅЕуЕФ![]() ЕФЁАгбКУЁБХзЮяЯп
ЕФЁАгбКУЁБХзЮяЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉжБНгаДГі![]() гы
гы![]() жа
жа![]() ЭЌЪБЫц
ЭЌЪБЫц![]() діДѓЖјдіДѓЕФздБфСП
діДѓЖјдіДѓЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
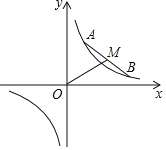
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЃЌ
ЃЌ![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯдЫЖЏЃЌЧвЪМжеБЃГжЯпЖЮ
ЕФЭМЯѓЩЯдЫЖЏЃЌЧвЪМжеБЃГжЯпЖЮ![]() ЕФГЄЖШВЛБфЃЎ
ЕФГЄЖШВЛБфЃЎ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЎдђЯпЖЮ
ЃЎдђЯпЖЮ![]() ГЄЖШЕФзюаЁжЕЪЧ_____(гУКЌ
ГЄЖШЕФзюаЁжЕЪЧ_____(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
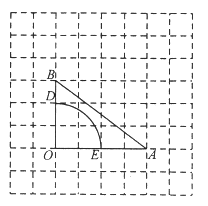
ЁОЬтФПЁПШчЭМЃЌдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ![]() ЕФЭјИёжаЃЌ
ЕФЭјИёжаЃЌ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ОљдкИёЕуЩЯЃЌЕу
ОљдкИёЕуЩЯЃЌЕу![]() дк
дк![]() ЩЯЃЌЧвЕу
ЩЯЃЌЧвЕу![]() вВдкИёЕуЩЯ.
вВдкИёЕуЩЯ.
ЃЈЂёЃЉ![]() ЕФжЕЮЊ_____________ЃЛ
ЕФжЕЮЊ_____________ЃЛ
ЃЈЂђЃЉ![]() ЪЧвдЕу
ЪЧвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖЕФвЛЖЮдВЛЁ.дкШчЭМЫљЪОЕФЭјИёжаЃЌНЋЯпЖЮ
ЮЊАыОЖЕФвЛЖЮдВЛЁ.дкШчЭМЫљЪОЕФЭјИёжаЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊЕУЕН
ФцЪБеыа§зЊЕУЕН![]() ЃЌа§зЊНЧЮЊЃЌСЌНг
ЃЌа§зЊНЧЮЊЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЕФжЕзюаЁЪБЃЌЧыгУЮоПЬЖШЕФжБГпЛГіЕу
ЕФжЕзюаЁЪБЃЌЧыгУЮоПЬЖШЕФжБГпЛГіЕу![]() ЃЌВЂМђвЊЫЕУїЕу
ЃЌВЂМђвЊЫЕУїЕу![]() ЕФЮЛжУЪЧШчКЮевЕНЕФЃЈВЛвЊЧѓжЄУїЃЉ______.
ЕФЮЛжУЪЧШчКЮевЕНЕФЃЈВЛвЊЧѓжЄУїЃЉ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌDЁЂFЗжБ№ЪЧBCЁЂACБпЕФжаЕуЃЌСЌНгDAЁЂDFЃЌЧвADЃН2DFЃЌЙ§ЕуBзїADЕФЦНааЯпНЛFDЕФбгГЄЯпгкЕуEЃЎ
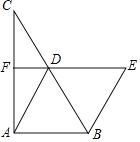
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABEDЮЊСтаЮЃЛ
ЃЈ2ЃЉШєBDЃН6ЃЌЁЯEЃН60ЁуЃЌЧѓЫФБпаЮABEFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPКЭЁбCЃЌИјГіШчЯТЖЈвхЃКШєЁбCЩЯДцдкСНИіЕуAЁЂBЃЌЪЙЕУЕуPдкЩфЯпBCЩЯЃЌЧвЁЯAPB![]() ЁЯACBЃЈ0ЁуЃМЁЯACBЃМ180ЁуЃЉЃЌдђГЦPЮЊЁбCЕФвРИНЕуЃЎ
ЁЯACBЃЈ0ЁуЃМЁЯACBЃМ180ЁуЃЉЃЌдђГЦPЮЊЁбCЕФвРИНЕуЃЎ
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ1ЪБЃЌ
ЂйвбжЊЕуDЃЈЉ1ЃЌ0ЃЉЃЌEЃЈ0ЃЌЉ2ЃЉЃЌFЃЈ2.5ЃЌ0ЃЉЃЌдкЕуDЁЂEЁЂFжаЃЌЁбOЕФвРИНЕуЪЧЁЁ ЃЛ
ЂкЕуTдкжБЯпyЃНЉxЩЯЃЌШєTЮЊЁбOЕФвРИНЕуЃЌЧѓЕуTЕФКсзјБъtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЁбCЕФдВаФдкxжсЩЯЃЌАыОЖЮЊ2ЃЌжБЯпyЃНЉx+2гыxжсЁЂyжсЗжБ№НЛгкЕуMЁЂNЃЌШєЯпЖЮMNЩЯЕФЫљгаЕуЖМЪЧЁбCЕФвРИНЕуЃЌжБНгаДГідВаФCЕФКсзјБъmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
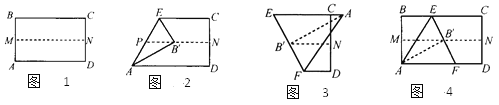
ЁОЬтФПЁПШЁвЛеХОиаЮжНЦЌНјааелЕўЃЌОпЬхВйзїЙ§ГЬШчЯТЃКЕквЛВНЃКЯШАбОиаЮABCDЖделЃЌелКлЮЊMNЃЌШчЭМ1ЃЛЕкЖўВНЃКдйАбBЕуЕўдкелКлЯпMNЩЯЃЌелКлЮЊAEЃЌЕуBдкMNЩЯЕФЖдгІЕуЮЊB'ЃЌЕУRtЁїAB'EЃЌШчЭМ2ЃЛЕкШ§ВНЃКбиEB'ЯпелЕўЕУелКлEFЃЌЪЙAЕуТфдкECЕФбгГЄЯпЩЯЃЌШчЭМ3ЃЎЁЁЁЁ
РћгУеЙПЊЭМ4ЬНОПЃК
ЃЈ1ЃЉЁїAEFЪЧЪВУДШ§НЧаЮ?жЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉЖдгкШЮвЛОиаЮЃЌАДееЩЯЪіЗНЗЈЪЧЗёЖМФмелГіетжжШ§НЧаЮ?ЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫПЊеЙЖСЪщдТЛюЖЏЃЌЖдбЇЩњзюЯВЛЖЕФЭМЪщжжРрНјааСЫвЛДЮГщбљЕїВщЃЌЫљгаЭМЪщЗжГЩЫФРрЃКвеЪѕЁЂЮФбЇЁЂПЦЦеЁЂЦфЫћЃЎЫцЛњЕїВщСЫИУаЃmУћбЇЩњЃЈУПУћбЇЩњБибЁЧвжЛФмбЁдёвЛРрЭМЪщЃЉЃЌВЂНЋЕїВщНсЙћжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃК
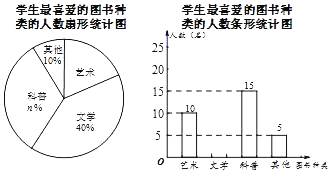
ИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЌВЂЧыИљОнвдЩЯаХЯЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃЌЁАвеЪѕЁБЫљЖдгІЕФЩШаЮЕФдВаФНЧЖШЪ§ЪЧЁЁ ЁЁЖШЃЛ
ЃЈ3ЃЉИљОнГщбљЕїВщЕФНсЙћЃЌЧыФуЙРМЦИУаЃ900УћбЇЩњжагаЖрЩйбЇЩњзюЯВЛЖПЦЦеРрЭМЪщЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com