
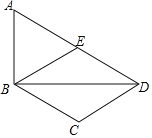
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=2,求AC的长.
【答案】(1)见解析.(2)2![]()
【解析】
(1)先证明四边形BCDE是平行四边形,再证明BE=DE,根据一组邻边相等的平行四边形为菱形即可判定四边形BCDE是菱形;(2)连接AC,根据平行线的性质及角平分线的定义证得∠BAC=∠DAC=∠BCA,即可得AB=BC=2,根据锐角三角函数的定义求得∠ADB=30°,所以∠DAC=30°,∠ADC=60°,在Rt△ACD中,即可求得AC=2![]() .
.
(1)证明:∵AD=2BC,E为AD的中点,
∴DE=BC,
∵AD∥BC,
∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,
∴BE=DE,
∴四边形BCDE是菱形.
(2)连接AC.
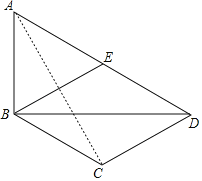
∵AD∥BC,AC平分∠BAD,
∴∠BAC=∠DAC=∠BCA,
∴AB=BC=2,
∵AD=2BC=4,
∴sin∠ADB=![]() ,
,
∴∠ADB=30°,
∵四边形BCDE是菱形.
∴∠DAC=30°,∠ADC=60°,
在Rt△ACD中,∵AD=4,
∴AC=2![]() .
.


科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.
其中,1和0既不是质数也不是合数.
材料二:一个较大自然数是质数还是合数通常用“![]() 法”来判断,主要分为三个步骤:
法”来判断,主要分为三个步骤:
第一步,找出大于![]() 且最接近
且最接近![]() 的平方数
的平方数![]() ;
;
第二步,用小于![]() 的所有质数去除
的所有质数去除![]() ;
;
第三步,如果这些质数都不能整除![]() ,那么
,那么![]() 是质数;如果这些质数中至少有一个能整除
是质数;如果这些质数中至少有一个能整除![]() ,那么
,那么![]() 就是合数.
就是合数.
如何判断239是质数还是合数?
第一步,![]() ;
;
第二步,小于16的质数有:2、3、5、7、11、13,用2、3、5、7、11、13依次去除239;
第三步,发现没有质数能整除239,所以239是质数.
材料三:分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(
…(![]() ,
,![]() ,
,![]() …是不相等的质数,
…是不相等的质数,![]() ,
,![]() ,
,![]() …是正整数),则合数
…是正整数),则合数![]() 共有
共有![]() …个约数.如
…个约数.如![]() ,
,![]() ,则8共有4个约数;又如
,则8共有4个约数;又如![]() ,
,![]() ,则12共有6个约数.请用以上方法解决下列问题:
,则12共有6个约数.请用以上方法解决下列问题:
(1)请用“![]() 法”判断163是质数还是合数;
法”判断163是质数还是合数;
(2)求有12个约数的最小自然数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y=![]() 的图象交于点C(﹣1,m).
的图象交于点C(﹣1,m).
(1)求一次函数和反比例函数的表达式;
(2)直接写出关于x的不等式2x+b>![]() 的解集;
的解集;
(3)点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
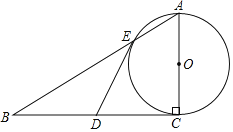
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光.
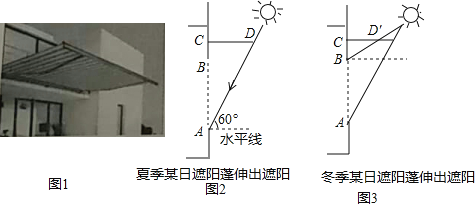
(1)计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)
(2)如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 也在抛物线
也在抛物线![]() 上(点
上(点![]() 与点
与点![]() 不重合),我们称这样的两条抛物线
不重合),我们称这样的两条抛物线![]() 、
、![]() 互为“友好”抛物线,如图1.
互为“友好”抛物线,如图1.
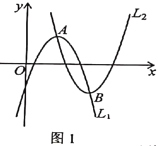
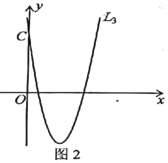
解决问题:如图2,已知物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称,求点
的对称轴对称,求点![]() 的坐标;
的坐标;
(2)求出以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式;
的解析式;
(3)直接写出![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A、B,使得点P在射线BC上,且∠APB![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时,
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D、E、F中,⊙O的依附点是 ;
②点T在直线y=﹣x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为2,直线y=﹣x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,直接写出圆心C的横坐标m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com