
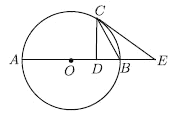
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨ń≥Õ¨—ßľ“Ķń“Ľ√śīįĽß…Ōį≤◊į”–’ŕ—ŰŇŮ£¨Õľ2ļÕÕľ3 «Ĺō√ś ĺ“‚Õľ£¨CD «’ŕ—ŰŇŮ£¨īįĽßABő™1.5√◊£¨BCő™0.5√◊£ģł√’ŕ—ŰŇŮ”–…žňűĻ¶ń‹£ģ»ÁÕľ2£¨ł√Õ¨—ß‘ŕŌńľĺń≥»’Ķń’żőÁ ĪŅŐ≤‚Ķ√Őę—ŰĻ‚ļÕňģ∆ĹŌŖĶńľ–Ĺ«ő™60°„£¨’ŕ—ŰŇŮCD’żļ√ĹęĹÝ»ŽīįĽßABĶń—ŰĻ‚Ķ≤◊°£Ľ»ÁÕľ3£¨ł√Õ¨—ß‘ŕ∂¨ľĺń≥»’Ķń’żőÁ ĪŅŐ≤‚Ķ√Őę—ŰĻ‚ļÕňģ∆ĹŌŖĶńľ–Ĺ«ő™30°„£¨Ĺę’ŕ—ŰŇŮ ’ňű≥…CD°š Ī£¨’ŕ—ŰŇŮ’żļ√ÕÍ»ę≤ĽĶ≤ĹÝ»ŽīįĽßABĶń—ŰĻ‚£ģ
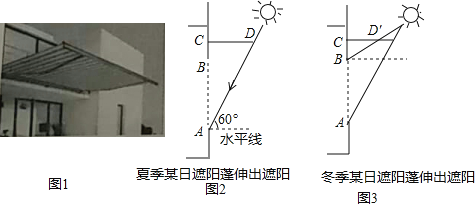
£®1£©ľ∆ň„Õľ3÷–CD°šĶń≥§∂»Ī»Õľ2÷–CDĶń≥§∂» ’ňűŃň∂ŗ…Ŕ√◊£Ľ£®ĹŠĻŻĪ£ŃŰłýļŇ£©
£®2£©»ÁĻŻÕľ3÷–’ŕ—ŰŇŮĶń≥§∂»ő™Õľ2÷–CDĶń≥§∂»£¨«Žľ∆ň„ł√’ŕ—ŰŇ٬š‘ŕīįĽßAB…ŌĶń“ű”į≥§∂»ő™∂ŗ…Ŕ√◊£Ņ£®«Ž‘ŕÕľ3÷–Ľ≠Õľ≤ĘĪÍ≥ŲŌŗ”¶◊÷ńł£¨»Ľļů‘Ŕľ∆ň„£©
°ĺīūįł°Ņ£®1£©Õľ3÷–CD°šĶń≥§∂»Ī»Õľ2÷–CDĶń≥§∂» ’ňűŃň![]() √◊£Ľ£®2£©ł√’ŕ—ŰŇ٬š‘ŕīįĽßAB…ŌĶń“ű”į≥§∂»ő™
√◊£Ľ£®2£©ł√’ŕ—ŰŇ٬š‘ŕīįĽßAB…ŌĶń“ű”į≥§∂»ő™![]() √◊£ģ
√◊£ģ
°ĺĹ‚őŲ°Ņ
£®1£©Ĺ‚÷ĪĹ«°ųACD£¨«ů≥ŲCD£¨‘ŔĹ‚÷ĪĹ«°ųBCD°š£¨«ů≥ŲCD°š£¨»Ľļůľ∆ň„CD©ĀCD°šĶń≥§∂»ľīŅ…£Ľ
£®2£©Õľ3÷–’ŕ—ŰŇÓĶń≥§∂»ő™Õľ2÷–CDĶń≥§∂» Ī£¨ĻżD◊ųDE°őBD°š£¨ĹĽAB”ŕE£¨Ĺ‚÷ĪĹ«°ųECD£¨«ů≥ŲCE£¨‘Ŕľ∆ň„CE-BCľīŅ…£ģ
£®1£©‘ŕ÷ĪĹ«°ųACD÷–£¨°ŖAC£ĹAB+BC£Ĺ2√◊£¨°ŌCAD£Ĺ30°„£¨
°ŗtan°ŌCAD£Ĺ![]() £¨
£¨
°ŗCD£ĹACtan°ŌCAD£Ĺ2°Ń![]() £Ĺ
£Ĺ![]() £®√◊£©£ģ
£®√◊£©£ģ
‘ŕ÷ĪĹ«°ųBCD°š÷–£¨°ŖBC£Ĺ0.5√◊£¨°ŌCBD°š£Ĺ60°„£¨
°ŗtan°ŌCBD°š£Ĺ![]() £¨
£¨
°ŗCD°š£ĹBCtan°ŌCBD°š£Ĺ0.5°Ń![]() £Ĺ
£Ĺ![]() £®√◊£©£¨
£®√◊£©£¨
°ŗCD©ĀCD°š£Ĺ![]() ©Ā
©Ā![]() £Ĺ
£Ĺ![]() £®√◊£©£ģ
£®√◊£©£ģ
Ļ Õľ3÷–CD°šĶń≥§∂»Ī»Õľ2÷–CDĶń≥§∂» ’ňűŃň![]() √◊£Ľ
√◊£Ľ
£®2£©»ÁÕľ£¨Õľ3÷–’ŕ—ŰŇŮĶń≥§∂»ő™Õľ2÷–CDĶń≥§∂» Ī£¨ĻżD◊ųDE°őBD°š£¨ĹĽAB”ŕE£ģ
‘ŕ÷ĪĹ«°ųECD÷–£¨°ŖCD£Ĺ![]() √◊£¨°ŌCED£Ĺ60°„£¨
√◊£¨°ŌCED£Ĺ60°„£¨
°ŗtan°ŌCED£Ĺ![]() £¨
£¨
°ŗCE£Ĺ![]() £Ĺ
£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŗBE£ĹCE©ĀBC£Ĺ![]() ©Ā0.5£Ĺ
©Ā0.5£Ĺ![]() £®√◊£©£ģ
£®√◊£©£ģ
Ļ ł√’ŕ—ŰŇ٬š‘ŕīįĽßAB…ŌĶń“ű”į≥§∂»ő™![]() √◊£ģ
√◊£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ń‚–ő![]() ÷–£¨
÷–£¨![]() ∑÷Īūő™
∑÷Īūő™![]() …ŌĶńĶ„£¨«“
…ŌĶńĶ„£¨«“![]() £¨Ń¨Ĺ”≤Ę—”≥§
£¨Ń¨Ĺ”≤Ę—”≥§![]() £¨”Ž
£¨”Ž![]() Ķń—”≥§ŌŖĹĽ”ŕĶ„
Ķń—”≥§ŌŖĹĽ”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £ģ
£ģ
£®1£©«ů÷§£ļňńĪŖ–ő![]() «∆Ĺ––ňńĪŖ–ő£Ľ
«∆Ĺ––ňńĪŖ–ő£Ľ
£®2£©Ń¨Ĺ”![]() £¨»Ű
£¨»Ű![]() £¨
£¨![]() £¨«ů
£¨«ů![]() Ķń≥§£ģ
Ķń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
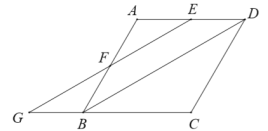
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨AD°őBC£¨CE∆Ĺ∑÷°ŌBCD£¨°ŌDAC£Ĺ3°ŌBCD£¨°ŌACD£Ĺ20°„£¨ĶĪAB”ŽACĽ•ŌŗīĻ÷Ī Ī£¨°ŌBĶń∂» żő™_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
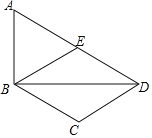
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńĪŖ–őABCD÷–£¨BDő™“ĽŐű∂‘Ĺ«ŌŖ£¨AD°őBC£¨AD£Ĺ2BC£¨°ŌABD£Ĺ90°„£¨Eő™ADĶń÷–Ķ„£¨Ń¨Ĺ”BE£ģ
£®1£©«ů÷§£ļňńĪŖ–őBCDEő™Ń‚–ő£Ľ
£®2£©Ń¨Ĺ”AC£¨»ŰAC∆Ĺ∑÷°ŌBAD£¨BC£Ĺ2£¨«ůACĶń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖ![]() ĺ≠Ļż
ĺ≠Ļż![]() £¨
£¨![]() ŃĹĶ„£¨«“”Ž
ŃĹĶ„£¨«“”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() £¨Ķ„
£¨Ķ„![]() «Ň◊őÔŌŖĶń∂•Ķ„£¨Ň◊őÔŌŖĶń∂‘≥∆÷Š
«Ň◊őÔŌŖĶń∂•Ķ„£¨Ň◊őÔŌŖĶń∂‘≥∆÷Š![]() ĹĽ
ĹĽ![]() ÷Š”ŕĶ„
÷Š”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £ģ
£ģ
£®1£©«ůĺ≠Ļż![]() £¨
£¨![]() £¨
£¨![]() »żĶ„ĶńŇ◊őÔŌŖĶńļĮ żĪŪīÔ Ĺ£Ľ
»żĶ„ĶńŇ◊őÔŌŖĶńļĮ żĪŪīÔ Ĺ£Ľ
£®2£©Ķ„![]() «ŌŖ∂ő
«ŌŖ∂ő![]() …Ō“ĽĶ„£¨ĶĪ
…Ō“ĽĶ„£¨ĶĪ![]() Ī£¨«ůĶ„
Ī£¨«ůĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨ĻżĶ„![]() ◊ų
◊ų![]() ÷Š”ŕĶ„
÷Š”ŕĶ„![]() £¨
£¨![]() ő™Ň◊őÔŌŖ…Ō“Ľ∂ĮĶ„£¨
ő™Ň◊őÔŌŖ…Ō“Ľ∂ĮĶ„£¨![]() ő™
ő™![]() ÷Š…Ō“Ľ∂ĮĶ„£¨
÷Š…Ō“Ľ∂ĮĶ„£¨![]() ő™÷ĪŌŖ
ő™÷ĪŌŖ![]() …Ō“Ľ∂ĮĶ„£¨ĶĪ“‘
…Ō“Ľ∂ĮĶ„£¨ĶĪ“‘![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() ő™∂•Ķ„ĶńňńĪŖ–ő «’ż∑Ĺ–ő Ī£¨«Ž«ů≥ŲĶ„
ő™∂•Ķ„ĶńňńĪŖ–ő «’ż∑Ĺ–ő Ī£¨«Ž«ů≥ŲĶ„![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ


≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
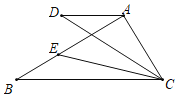
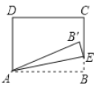
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕĺō–ő![]() ÷–£¨
÷–£¨![]() Ķ„
Ķ„![]() ő™…šŌŖ
ő™…šŌŖ![]() …Ō“Ľ∂ĮĶ„£¨Ĺę
…Ō“Ľ∂ĮĶ„£¨Ĺę![]() —ō
—ō![]() ’ŘĶĢ£¨Ķ√ĶĹ
’ŘĶĢ£¨Ķ√ĶĹ![]() »Ű
»Ű![]() «°ļ√¬š‘ŕ…šŌŖ
«°ļ√¬š‘ŕ…šŌŖ![]() …Ō£¨‘Ú
…Ō£¨‘Ú![]() Ķń≥§ő™________£ģ
Ķń≥§ő™________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕĪŖ≥§ő™4Ķń’ż∑Ĺ–ő![]() ÷–£¨
÷–£¨![]() «
«![]() ĪŖ…ŌĶńŃĹłŲ∂ĮĶ„£¨«“
ĪŖ…ŌĶńŃĹłŲ∂ĮĶ„£¨«“![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨
£¨![]() ”Ž
”Ž![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨Ō¬Ń–ĹŠ¬Ř£ļĘŔ
£¨Ō¬Ń–ĹŠ¬Ř£ļĘŔ![]() £ĽĘŕ
£ĽĘŕ![]() ∆Ĺ∑÷
∆Ĺ∑÷![]() £ĽĘŘ
£ĽĘŘ![]() £ĽĘ‹
£ĽĘ‹![]() £ĽĘ›ŌŖ∂ő
£ĽĘ›ŌŖ∂ő![]() Ķń◊Ó–°÷Ķ «
Ķń◊Ó–°÷Ķ «![]() £ģ’ż»∑ĶńłŲ ż”–£® £©
£ģ’ż»∑ĶńłŲ ż”–£® £©
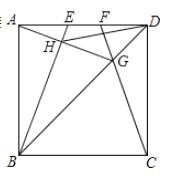
A.2łŲB.3łŲC.4łŲD.5łŲ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
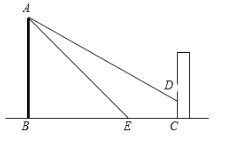
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ń≥Ļę‘įńŕ”–“Ľ◊ýĻŇňĢAB£¨‘ŕňĢĶńĪĪ√ś”–“Ľ∂įĹ®÷ĢőÔ£¨ń≥»’…ŌőÁ9 ĪŐę—ŰĻ‚ŌŖ”Žňģ∆Ĺ√śĶńľ–Ĺ«ő™32°„£¨īň ĪňĢ‘ŕĹ®÷ĢőÔĶń«Ĺ…ŌŃŰŌ¬ŃňłŖ3√◊Ķń”į◊”CD£ģ÷–őÁ12 ĪŐę—ŰĻ‚ŌŖ”ŽĶō√śĶńľ–Ĺ«ő™45°„£¨īň ĪňĢľ‚A‘ŕĶō√ś…ŌĶń”į◊”E”Ž«ĹĹ«CĶńĺŗņŽő™15√◊£®B°ĘE°ĘC‘ŕ“ĽŐű÷ĪŌŖ…Ō£©£¨«ůňĢABĶńłŖ∂»£ģ£®ĹŠĻŻĺę»∑ĶĹ0.01√◊£©
≤őŅľ żĺ›£ļsin32°„°÷0.5299£¨cos32°„°÷0.8480£¨tan32°„°÷0.6249£¨![]() £ģ
£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() ő™
ő™![]() Ķń÷Īĺ∂£¨
Ķń÷Īĺ∂£¨![]() ő™
ő™![]() …Ō“ĽĶ„£¨Ń¨Ĺ”
…Ō“ĽĶ„£¨Ń¨Ĺ”![]() £¨Ļż
£¨Ļż![]() ◊ų
◊ų![]() ”ŕĶ„
”ŕĶ„![]() £¨ĻżĶ„
£¨ĻżĶ„![]() ◊ų
◊ų![]() £¨∆š÷–
£¨∆š÷–![]() ĹĽ
ĹĽ![]() Ķń—”≥§ŌŖ”ŕĶ„
Ķń—”≥§ŌŖ”ŕĶ„![]() £ģ
£ģ
£®1£©«ů÷§£ļ![]() «
«![]() Ķń«–ŌŖ£ģ
Ķń«–ŌŖ£ģ
£®2£©»ÁÕľ£¨Ķ„![]() ‘ŕ
‘ŕ![]() …Ō£¨«“¬ķ◊„
…Ō£¨«“¬ķ◊„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() ≤Ę—”≥§ĹĽ
≤Ę—”≥§ĹĽ![]() Ķń—”≥§ŌŖ”ŕĶ„
Ķń—”≥§ŌŖ”ŕĶ„![]() £ģ
£ģ
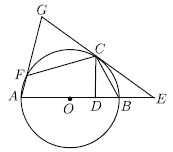
ĘŔ ‘ŐĹĺŅŌŖ∂ő![]() ”Ž
”Ž![]() ÷ģľš¬ķ◊„Ķń żŃŅĻōŌĶ£ģ
÷ģľš¬ķ◊„Ķń żŃŅĻōŌĶ£ģ
Ęŕ»Ű![]() £¨
£¨![]() £¨«ůŌŖ∂ő
£¨«ůŌŖ∂ő![]() Ķń≥§£ģ
Ķń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com