
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
【答案】(1)见解析;(2)BF=![]() .
.
【解析】
(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是菱形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为等腰直角三角形,求出BD的长,由BD﹣DF求出BF的长即可.
解:(1)由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
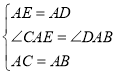 ,
,
∴△AEC≌△ADB(SAS);
(2)∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:AB=AD,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴BD2=2AB2,即BD=2![]() ,
,
∴AD=DF=FC=AC=AB=2,
∴BF=BD﹣DF=2![]() ﹣2.
﹣2.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
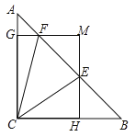
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上两动点,且
上两动点,且![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)试探究![]() 、
、![]() 、
、![]() 之间有何数量关系?说明理由.
之间有何数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
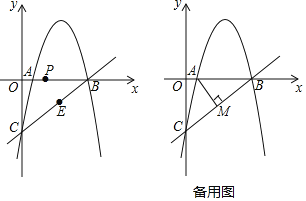
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=
(x>0)的图象与直线y=![]() x+1交于点A(2,m).
x+1交于点A(2,m).
(1)求k、m的值;
(2)已知点P(n,0),过点P作平行于 y 轴的直线,交直线y=![]() x+1于点B,交函数y=
x+1于点B,交函数y=![]() (x>0)的图象于点C.若y=
(x>0)的图象于点C.若y=![]() (x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
(x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
①当n=4时,直接写出图形G的整点坐标;
②若图形G 恰有2 个整点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中实线所示,函数y=|a(x﹣1)2﹣1|的图象经过原点,小明同学研究得出下面结论:
①a=1;②若函数y随x的增大而减小,则x的取值范围一定是x<0;
③若方程|a(x﹣1)2﹣1|=k有两个实数解,则k的取值范围是k>1;
④若M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函数图象的四个不同点,且m1<m2<m3<m4,则有m2+m3﹣m1=m4.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
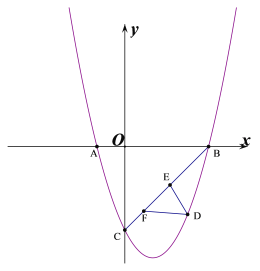
【题目】如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式.
(2)如图,直线BC下方的抛物线上有一点D,过点D作DE⊥BC于点E,作DF平行x轴交直线BC于点F,求△DEF周长的最大值.
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线对称轴的右侧,是否存在以点P,M,N,Q为顶点且以PM为边的正方形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为![]() 米的点
米的点![]() 处.这时,一辆出租车由西向东匀速行驶,测得此车从
处.这时,一辆出租车由西向东匀速行驶,测得此车从![]() 处行驶到
处行驶到![]() 处所用的时间为
处所用的时间为![]() 秒,且
秒,且![]() ,
,![]() .
.

![]() 求
求![]() 、
、![]() 之间的路程;
之间的路程;
![]() 请判断此出租车是否超过了城南大道每小时
请判断此出租车是否超过了城南大道每小时![]() 千米的限制速度?
千米的限制速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(-1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)求这个二次函数的表达式;
(2)点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
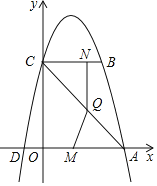
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com