
【题目】如图中实线所示,函数y=|a(x﹣1)2﹣1|的图象经过原点,小明同学研究得出下面结论:
①a=1;②若函数y随x的增大而减小,则x的取值范围一定是x<0;
③若方程|a(x﹣1)2﹣1|=k有两个实数解,则k的取值范围是k>1;
④若M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函数图象的四个不同点,且m1<m2<m3<m4,则有m2+m3﹣m1=m4.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】
①根据函数图像经过原点![]() ,可得
,可得![]() ;②由函数的图像可知:顶点坐标(1,1),与x轴的交点坐标(0,0),(2,0),当
;②由函数的图像可知:顶点坐标(1,1),与x轴的交点坐标(0,0),(2,0),当![]() 或
或![]() 时,函数y随x的增大而减小;③若方程
时,函数y随x的增大而减小;③若方程![]() 有两个实数解,
有两个实数解,![]() 或
或![]() ;④由函数的图像可知,直线
;④由函数的图像可知,直线![]() )与函数
)与函数![]() 的图像有四个交点,由m1<m2<m3<m4
的图像有四个交点,由m1<m2<m3<m4
可知![]() ,移项可得
,移项可得![]() .
.
解:(1)∵函数![]() 图像经过原点,
图像经过原点,
∴![]() ,
,
解得:![]() ,故①正确;
,故①正确;
(2)由函数图像可知顶点坐标(1,1),与x轴的交点坐标(0,0),(2,0),
∵函数y随x的增大而减小,
∴![]() 或
或![]() ,故②错误;
,故②错误;
(3)∵方程![]() 有两个实数解,
有两个实数解,
∴![]() 或
或![]() ,故③错误;
,故③错误;
(4)∵M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函数图象的四个不同点,
∴直线![]() 自变量取值范围为
自变量取值范围为![]() )
)
∴m1与m4,m2与m3关于x=1对称,
∴![]() ,即
,即![]() ,
,
故④正确;
故答案为:C.


科目:初中数学 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式x2+
,求代数式x2+![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() =4
=4
即![]() =4∴x+
=4∴x+![]() =4∴x2+
=4∴x2+![]() =(x+
=(x+![]() )2﹣2=16﹣2=14
)2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求![]() 的值.
的值.
解:令2x=3y=4z=k(k≠0)
则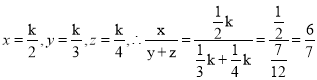
根据材料回答问题:
(1)已知![]() ,求x+
,求x+![]() 的值.
的值.
(2)已知![]() ,(abc≠0),求
,(abc≠0),求![]() 的值.
的值.
(3)若![]() ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.

(1)如图1,△ABC的两内角∠ABC与∠ACB的平分线交于点E,求证:∠BEC=90°+![]() ∠A;
∠A;
(2)如图2,△ABC的内角∠ABC的平分线与△ABC的外角∠ACM的平分线交于点E,请写出∠E与∠A的数量关系,并证明.
(3)如图3,△ABC的两外角∠DBC与∠BCF的平分线交于点E,请你直接写出∠E与∠A的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线.
(1)求证:CE=CB;
(2)连接AF,BF,求∠ABF的正弦值;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com