
【题目】某学校体育社团活动计划开设“足球、篮球、排球、乒乓球”四个体育兴趣小组,每个学生只能选报一项参加活动,为了解该社团成员选择兴趣小组的情况,某调查小组在社团中进行了一次抽样调查,绘制了如下尚不完整的统计图表.
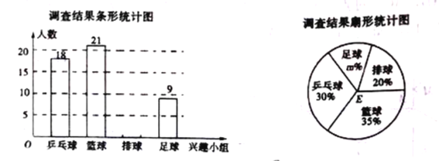
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量为 ,扇形统计图中的值为 .
(2)补全条形统计图;
(3)若该学校有学生![]() 人,有
人,有![]() 的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
(1)求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
(2)一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?
(3)为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以顶点
,以顶点![]() 为圆心,适当长为半径画弧,分别交边
为圆心,适当长为半径画弧,分别交边![]() 于点
于点![]() ;再分别以
;再分别以![]() 为圆心,以大于
为圆心,以大于![]() 为半径作弧,两弧在
为半径作弧,两弧在![]() 内交于点
内交于点![]() ;作射线
;作射线![]() 交边
交边![]() 于点
于点![]() 若
若![]() ,则
,则![]() 的面积为( )
的面积为( )
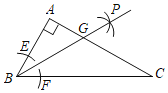
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行 随机抽样的问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”、“D.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2), 请根据图中的信息解答下列问题.
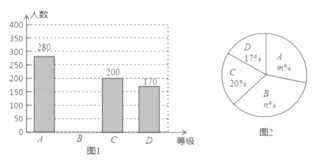
(1)这次调查的市民人数为________人,图2中,![]() _________;
_________;
(2)图1中的条形统计图中B等级的人数;
(3)在图2中的扇形统计图中,求“C.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“A.非常了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:
求证:
证明:
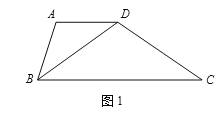
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中,作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)
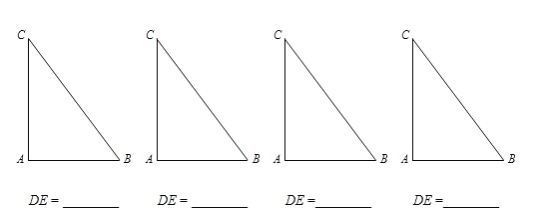
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,与抛物线
,与抛物线![]() 交于点
交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是线段
是线段![]() 上(不与
上(不与![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作矩形
为边作矩形![]() ,请求出矩形
,请求出矩形![]() 周长的最大值;
周长的最大值;
(3)若点![]() 在
在![]() 轴正半轴上,当
轴正半轴上,当![]() 恰好是等腰三角形时,请直接写出点
恰好是等腰三角形时,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
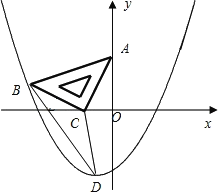
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
(1)点A的坐标为 ,点B的坐标为 ;抛物线的解析式为 ;
(2)设抛物线的顶点为D,求△DBC的面积;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
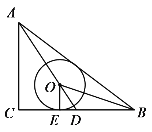
【题目】如图,![]() ABC中,∠C=90°,AC=6,AB=10,点O在BC边的中线AD上,OB 平分∠ABC,⊙O与BC相切于点E.
ABC中,∠C=90°,AC=6,AB=10,点O在BC边的中线AD上,OB 平分∠ABC,⊙O与BC相切于点E.
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
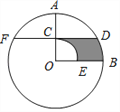
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.则图中阴影部分的面积为______________.
,交OB于E点.则图中阴影部分的面积为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com