
����Ŀ��Ϊ�˽�����ԡ���������֪ʶ����֪���̶ȣ�ij��ѧѧϰ��ȤС���������� ����������ʾ����飬��������Ϊ��A.�dz��˽⡱����B.�˽⡱����C.�����˽⡱����D.��̫�˽⡱�ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����������������ͳ��ͼ��ͼ1��ͼ2���� �����ͼ�е���Ϣ����������⣮
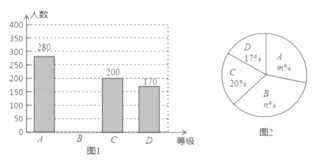
��1����ε������������Ϊ________�ˣ�ͼ2�У�![]() _________��
_________��
��2��ͼ1�е�����ͳ��ͼ��B�ȼ���������
��3����ͼ2�е�����ͳ��ͼ�У���C.�����˽⡱�������ε�Բ�ĽǶ�����
��4����ͳ�ƣ�2018�����Լ������500���ˣ���ô���ݳ�������Ľ�����ɹ��ƶԡ���������֪ʶ����֪���̶�Ϊ��A.�dz��˽⡱������Լ�ж������ˣ�
���𰸡���1��1000��35����2��350����3��72�㣻��4��Լ��140����
��������
��1��������ͳ��ͼ��C�ȼ���������������ͳ��ͼ��C�ȼ���ռ�ٷֱȼ���������ε������������A�ȼ������������������������m��Ȼ����1��ȥ���������ȼ���ռ�ٷֱȼ������n��
��2������������n%��ΪB�ȼ���������
��3����360����C�ȼ���ռ�ٷֱȼ�����������
��4����500����A�ȼ���ռ�ٷֱȼ��ý����
�⣺��1����ε������������Ϊ![]() ���ˣ���
���ˣ���
![]() ��
��
![]() ��
��
�ʴ�Ϊ��1000��35��
��2��![]() ���ˣ���
���ˣ���
��![]() �ȼ���������350�ˣ�
�ȼ���������350�ˣ�
��3��![]() ��
��
�𣺡�C�������˽⡱�������ε�Բ�ĽǶ���Ϊ72����
��4����������ã�![]() �����ˣ���
�����ˣ���
�𣺹��ƶԡ���������֪ʶ����֪���̶�Ϊ��A���dz��˽⡱������Լ��140���ˣ�
���ȼ���
���⿼��������ͳ��ͼ������ͳ��ͼ�������������������֪ʶ�����ڻ������ͣ���ȷ�������⡢����������������֪ʶ�ǽ���Ĺؼ���


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ڽ���
�ڽ���![]() ����
����![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() ��
��
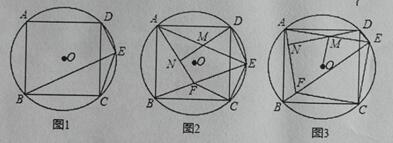
(1)��ͼ1����֤:��DEC+��BEC= 180�㣻
(2)��ͼ2������C��CF��CE��BE�ڵ�F������AF�� MΪAE���е㣬����DM���ӳ���AF�ڵ�N����֤: DN��AF��
(3)��ͼ3����(2) �������£�����OM����AB=10��![]() ��OM�ij���
��OM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У��Ե�P��2��a��ΪԲ�ĵġ�P��y�����У�ֱ��y��x���P�ཻ�ڵ�A��B����AB�ij�Ϊ2![]() ����a��ֵΪ_____��
����a��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϵ�һ����(�����
�ϵ�һ����(�����![]() �غ�)������
�غ�)������![]() ��
��![]() ���Ҳ���
���Ҳ���![]() Ϊб��������ֱ��������
Ϊб��������ֱ��������![]() .��
.��![]() ��
��![]() ���е㣬����
���е㣬����![]() .
.
[���ⷢ��]
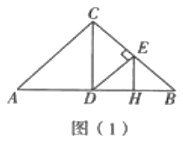
��1����ͼ(1)������![]() ��
��![]() ���е�ʱ���߶�
���е�ʱ���߶�![]() ��
��![]() ��������ϵ��______��
��������ϵ��______��![]() ��
��![]() ��λ�ù�ϵ��______��
��λ�ù�ϵ��______��
 ��
��
[������֤]
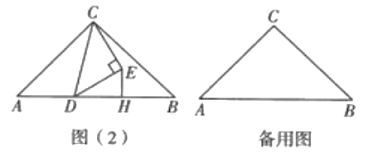
��2����ͼ��2��������![]() �ڱ�
�ڱ�![]() ���Ҳ���
���Ҳ���![]() ���е�ʱ��(1)�еĽ����Ƿ���Ȼ�������������������ͼ��2���е��������֤����������������˵�����ɣ�
���е�ʱ��(1)�еĽ����Ƿ���Ȼ�������������������ͼ��2���е��������֤����������������˵�����ɣ�
[��չӦ��]
��3����![]() �������������䣬����
�������������䣬����![]() .��
.��![]() �ǵȱ�������ʱ����ֱ��д��
�ǵȱ�������ʱ����ֱ��д��![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
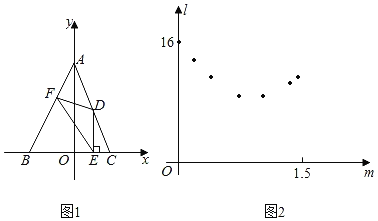
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���ABC�Ķ���A��C�քe��ֱ��y=��![]() x+4��������Ľ��㣬��B������Ϊ����2��0������D�DZ�AC�ϵ�һ�㣬DE��BC�ڵ�E����F�ڱ�AB�ϣ���D��F�������y���ϵ�ij������ĶԳƣ�����DF��EF�����D�ĺ�����Ϊm��EF2Ϊl����̽����
x+4��������Ľ��㣬��B������Ϊ����2��0������D�DZ�AC�ϵ�һ�㣬DE��BC�ڵ�E����F�ڱ�AB�ϣ���D��F�������y���ϵ�ij������ĶԳƣ�����DF��EF�����D�ĺ�����Ϊm��EF2Ϊl����̽����
���߶�EF�����Ƿ�����Сֵ��
�ڡ�BEF�ܷ��Ϊֱ�������Σ�
С�����������۲쩁���멁��֤��Ӧ�����ķ�������̽��������һ����������⣮
��1��С�����������λ������������й۲죬�������õ�l��m�仯��һ���Ӧֵ������ƽ��ֱ������ϵ���Ը���ӦֵΪ������㣨��ͼ2����������ͼ2�����ߣ��۲�ͼ������������l��m��������ĺ������
��2��С�����ͼ1������Ӧ�������κͺ���֪ʶ����֤��1���еIJ��룬�������l����m�ĺ�������ʽ���Ա�����ȡֵ��Χ��������߶�EF���ȵ���Сֵ��
��3��С��ͨ���۲죬���������֡�BEF�ܳ�Ϊֱ�������Σ������������BEFΪֱ��������ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Դ�����ḻ��������ѡ����������ѧϰ������ѧϰ��ʽ�������Ķ����������Ρ����ߴ��⡢�������ۣ��ô���ѧ�����꼶�����ȡ����ѧ�������������������ѧϰ��ʽ�����Ȥ���ĵ���(ÿλͬѧֻ��ѡһ��)�������ݵ��������Ƴ�����������������ͳ��ͼ������ͼ����Ϣ������������⣺
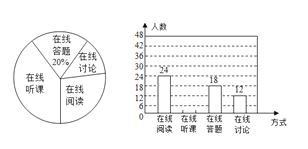
��1����ȫ����ͳ��ͼ��
��2��������ͳ��ͼ���������Ķ�����Ӧ������Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�������Ż�ƻ�������������������ƹ�������ĸ�������ȤС�飬ÿ��ѧ��ֻ��ѡ��һ��μӻ��Ϊ�˽�����ų�Աѡ����ȤС��������ij����С���������н�����һ�γ������飬�����������в�������ͳ��ͼ����
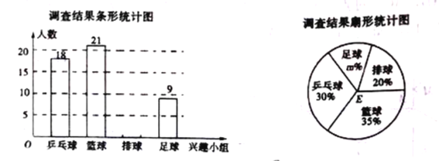
����������Ϣ����������⣺
��1�����γ����������������Ϊ ������ͳ��ͼ�е�ֵΪ ��
��2����ȫ����ͳ��ͼ��
��3������ѧУ��ѧ��![]() �ˣ���
�ˣ���![]() ��ѧ��ѡ���˲μ��������Ż��������Ƹ�Уѡ�������������������ȤС���ѧ����Լ���ж����ˣ�
��ѧ��ѡ���˲μ��������Ż��������Ƹ�Уѡ�������������������ȤС���ѧ����Լ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ��ҵ�ؼ��紴ҵ����һ����ֲ�辰�뻨�ܸ�50���ۺ�ͳ�����辰��ƽ��ÿ��������160Ԫ�����ܵ�ƽ��ÿ��������19Ԫ�����з��֣�
���辰ÿ����1�����辰��ƽ��ÿ���������2Ԫ;ÿ����1�����辰��ƽ��ÿ����������2Ԫ;�ڻ��ܵ�ƽ��ÿ������ʼ�ղ���.
С���ƻ��ڶ�����ֲ�辰�뻨�ܹ�100��������ֲ���辰�ȵ�һ������x�����ڶ����辰�뻨������������ֱ�ΪW1��W2����λ��Ԫ��
��1���ú�x�Ĵ���ʽ�ֱ��ʾW1��W2;
��2����xȡ��ֵʱ���ڶ�����ֲ���辰�뻨��������õ�������W���������������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O���ߣ��е�ΪA��OB���O����E��C��D��Բ�ϵ����㣬��CAƽ�֡�DCE����AB��![]() ����B��30������DE�ij���_____��
����B��30������DE�ij���_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com