练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

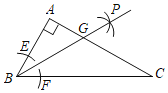
    【题目】如图，在中，，以顶点为圆心，适当长为半径画弧，分别交边于点；再分别以为圆心，以大于为半径作弧，两弧在内交于点；作射线交边于点若，则的面积为（ ）

    A.B.C.D.

    【答案】A

    【解析】

    作GH⊥BC于H，如图，利用基本作法得BP平分∠ABC，根据角平分线的性质得GA=GH=，再利用含30度的直角三角形三边的关系求出AB、BC，然后利用三角形面积公式求解．

    解：作GH⊥BC于H，如图，
    由作法得BP平分∠ABC，
    ∴GA=GH=，

    ∵∠A=90°，∠ABC=2∠C，
    ∴∠ABC=60°，∠C=30°，
    在Rt△ABG，

    ∵∠ABG=∠ABC=30°，
    ∴AB=AG=3，
    在Rt△ABC中，BC=2AB=6，
    ∴S△BCG=×6×=3，

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线与一次函数的图象交于点与反比例函数的图象交于点，点与点关于轴对称．

    （1）直接写出点的坐标；

    （2）求点的坐标（用含的式子表示）；

    （3）若两点中只有一个点在线段上，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现

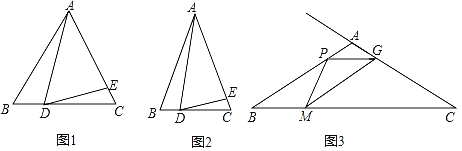
    如图1，ABC是等边三角形，点D，E分别在边BC，AC上，若∠ADE＝60°，则AB，CE，BD，DC之间的数量关系是　 　．

    （2）拓展探究

    如图2，ABC是等腰三角形，AB＝AC，∠B＝α，点D，E分别在边BC，AC上．若∠ADE＝α，则（1）中的结论是否仍然成立？请说明理由．

    （3）解决问题

    如图3，在ABC中，∠B＝30°，AB＝AC＝4cm，点P从点A出发，以1cm/s的速度沿A→B方向勾速运动，同时点M从点B出发，以cm/s的速度沿B→C方向匀速运动，当其中一个点运动至终点时，另一个点随之停止运动，连接PM，在PM右侧作∠PMG＝30°，该角的另一边交射线CA于点G，连接PC．设运动时间为t（s），当△APG为等腰三角形时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系中，以点P（2，a）为圆心的⊙P与y轴相切，直线y＝x与⊙P相交于点A、B，且AB的长为2，则a的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A(-2，4)，B(-2，1)，C(-5，2)．

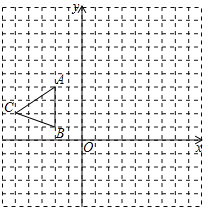
    （1）请画出△ABC关于x轴对称的△A1B1C1；

    （2）将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2，得到对应的点A2，B2，C2，请画出△A2B2C2；

    （3）△A1B1C1与△A2B2C2面积之比为 (不写解答过程，直接写出结果)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，点是直线上的一动点(不与点重合)，连接在的右侧以为斜边作等腰直角三角形.点是的中点，连接.

    [问题发现]

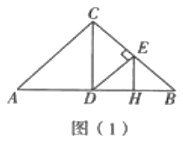
    （1）如图(1)，当点是的中点时，线段与的数量关系是______，与的位置关系是______；

    　

    [猜想论证]

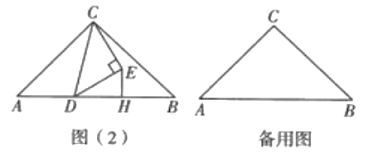
    （2）如图（2），当点在边上且不是的中点时，(1)中的结论是否仍然成立？若成立，请仅就图（2）中的情况给出证明；若不成立，请说明理由．

    [拓展应用]

    （3）若，其他条件不变，连接.当是等边三角形时，请直接写出的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

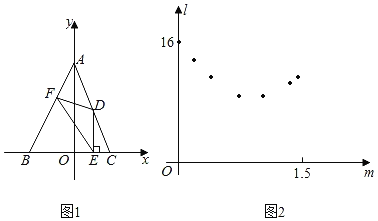
    【题目】如图1，在平面直角坐标系中，△ABC的顶点A，C分別是直线y=﹣x+4与坐标轴的交点，点B的坐标为（﹣2，0），点D是边AC上的一点，DE⊥BC于点E，点F在边AB上，且D，F两点关于y轴上的某点成中心对称，连结DF，EF．设点D的横坐标为m，EF2为l，请探究：

    ①线段EF长度是否有最小值．

    ②△BEF能否成为直角三角形．

    小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究，请你一起来解决问题．

    （1）小明利用“几何画板”软件进行观察，测量，得到l随m变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图2）．请你在图2中连线，观察图象特征并猜想l与m可能满足的函数类别．

    （2）小明结合图1，发现应用三角形和函数知识能验证（1）中的猜想，请你求出l关于m的函数表达式及自变量的取值范围，并求出线段EF长度的最小值．

    （3）小明通过观察，推理，发现△BEF能成为直角三角形，请你求出当△BEF为直角三角形时m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校体育社团活动计划开设“足球、篮球、排球、乒乓球”四个体育兴趣小组，每个学生只能选报一项参加活动，为了解该社团成员选择兴趣小组的情况，某调查小组在社团中进行了一次抽样调查，绘制了如下尚不完整的统计图表．

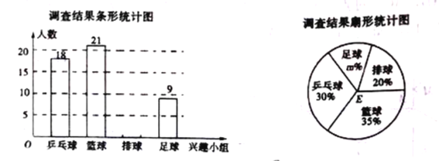
    根据以上信息解答下列问题：

    （1）本次抽样调查的样本容量为 ，扇形统计图中的值为 ．

    （2）补全条形统计图；

    （3）若该学校有学生人，有的学生选择了参加体育社团活动，请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，的直径为，点在圆周上（异于，），．

    （1）若，，求图中扇形的面积．

    （2）若是的平分线，求证：直线是的切线．

    查看答案和解析>>

    同步练习册答案