
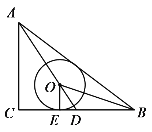
【题目】如图,![]() ABC中,∠C=90°,AC=6,AB=10,点O在BC边的中线AD上,OB 平分∠ABC,⊙O与BC相切于点E.
ABC中,∠C=90°,AC=6,AB=10,点O在BC边的中线AD上,OB 平分∠ABC,⊙O与BC相切于点E.
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)作OF垂直AB于点F,然后根据角平分线的性质定理即可证得OE=OF,从而证得结论;
(2)根据勾股定理求得BC,进而求得CD=DB=2,设⊙O的半径为r,然后根据S△ACD+S△COB+S△AOB=S△ABC,得到![]() ACCD+
ACCD+![]() BDr+
BDr+![]() ACBC,解关于r的方程即可求得半径;
ACBC,解关于r的方程即可求得半径;
(3)证得Rt△ODE∽Rt△ADC,根据相似三角形的性质求得DE=![]() ,即可求得BF=BE=
,即可求得BF=BE=![]() ,AF=AB-BF=
,AF=AB-BF=![]() ,解直角三角形即可求得
,解直角三角形即可求得![]() .
.
解:(1)证明:如图,作OF⊥AB于点F,
∵⊙O与BC相切于点E,
∴OE⊥BC
又∵OB 平分∠ABC
∴OE=OF,
∴AB为⊙O的切线
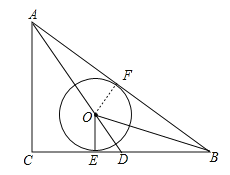
(2)∵∠C=90°,AC=6,AB=10,
∴由勾股定理得BC=8,
又D为BC的中点,
∴CD=DB=4,
设⊙O的半径为r,
∵S△ACD+S△BOD+S△AOB=S△ABC
∴12+2r+5r=24 ,解得r=![]()
∴⊙O的半径为![]()
(3)解:∵∠C=90°,OE⊥BC,
∴OE∥AC,
∴Rt△ODE∽Rt△ADC,
∴![]() ,
,
∴DE=![]() ,
,
又OE=OF,OB=OB
∴Rt△BOE≌Rt△BOF
∴BF=BE=![]() ,
,
∴AF=AB﹣BF=![]()
∴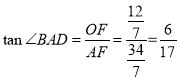 ./span>
./span>


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校体育社团活动计划开设“足球、篮球、排球、乒乓球”四个体育兴趣小组,每个学生只能选报一项参加活动,为了解该社团成员选择兴趣小组的情况,某调查小组在社团中进行了一次抽样调查,绘制了如下尚不完整的统计图表.
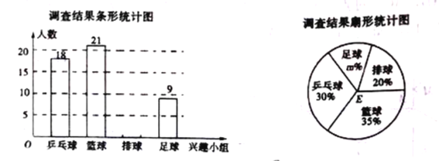
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量为 ,扇形统计图中的值为 .
(2)补全条形统计图;
(3)若该学校有学生![]() 人,有
人,有![]() 的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
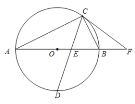
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,![]() 月
月![]() 日是母亲节,浩浩去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支
日是母亲节,浩浩去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支![]() 元,兰花每支
元,兰花每支![]() 元,浩浩只有
元,浩浩只有![]() 元,还想留着
元,还想留着![]() 元购买卡片.希望购买花的支数为
元购买卡片.希望购买花的支数为![]() 支,其中至少有一支是兰花.浩浩一共有多少种可能的购买方案?列出所有方案.
支,其中至少有一支是兰花.浩浩一共有多少种可能的购买方案?列出所有方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com