
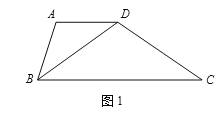
【题目】我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:
求证:
证明:
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中,作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)
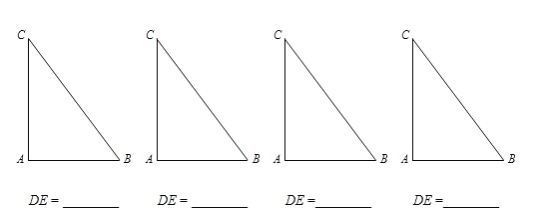
【答案】(1)答案见解析;(2)答案见解析.
【解析】
(1)根据准菱形的定义写出已知,结合图形写出求证,利用平行线的性质定理进行证明;
(2)分AE=AB,DE∥AB、BA=BD,DE∥AB、EA=ED,DE∥AB、DE=BD,DE∥AB四种情况,利用相似三角形的判定定理和性质定理计算即可.
(1)已知:如图,“准菱形”ABCD中,AB=AD,AD∥BC,(![]() ).
).
求证:BD平分∠ABC.
证明:∵AB=AD,
∴∠ABD=∠BDA.
又∵AD∥BC,
∴∠DBC=∠BDA,
∴∠ABD=∠DBC.
即BD平分∠ABC.
(2)可以作出如下四种图形:
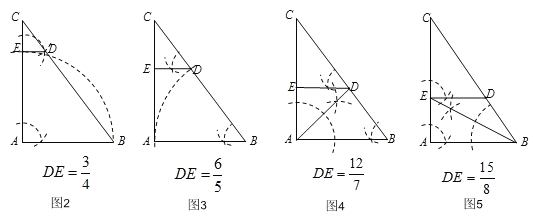
(2)可以作出如下四种图形,
∵∠A=90°,AB=3,AC=4,
∴BC=5,
如图2,当AE=AB,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
如图3,当BA=BD,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
如图4,当EA=ED,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
如图5,当DE=BD,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() .
.
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() .射线
.射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .过
.过![]() 点作
点作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过
.过![]() 点作半圆
点作半圆![]() 的切线
的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ∽
∽![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
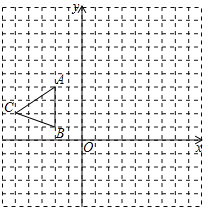
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)△A1B1C1与△A2B2C2面积之比为 (不写解答过程,直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
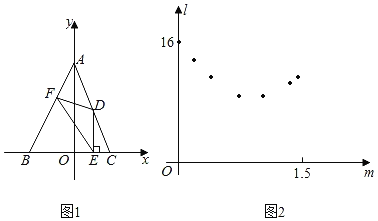
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
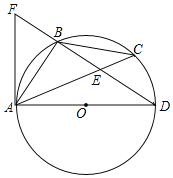
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校体育社团活动计划开设“足球、篮球、排球、乒乓球”四个体育兴趣小组,每个学生只能选报一项参加活动,为了解该社团成员选择兴趣小组的情况,某调查小组在社团中进行了一次抽样调查,绘制了如下尚不完整的统计图表.
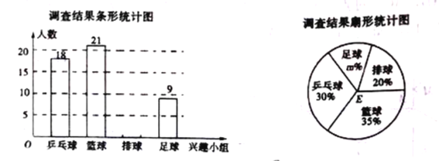
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量为 ,扇形统计图中的值为 .
(2)补全条形统计图;
(3)若该学校有学生![]() 人,有
人,有![]() 的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 和
和![]() 在第一象限内的图象如图所示,点P是
在第一象限内的图象如图所示,点P是![]() 的图象上一动点,作PC⊥x轴于点C,交
的图象上一动点,作PC⊥x轴于点C,交![]() 的图象于点A,作PD⊥y轴于点D,交
的图象于点A,作PD⊥y轴于点D,交![]() 的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )

A.①③B.②③④C.①③④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
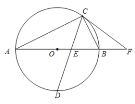
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OA是⊙O的半径,OA=1,点P是OA上一动点,过P作弦BC⊥OA,连接AB、AC.
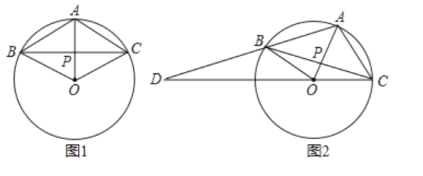
(1)如图1,若P为OA中点,则AC=______,∠ACB=_______°;
(2)如图2,若移动点P,使AB、CO的延长线交于点D.记△AOC的面积为S1,△BOD的面积为S2.△AOD的面积为S3,且满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com