
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
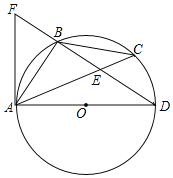
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
【答案】(1)见解析;(2)![]()
【解析】
(1)由圆周角定理得出∠ABD=90°,∠C=∠D,证出∠BAD+∠BAF=90°,得出AF⊥AD,即可得出结论;
(2)由圆周角定理得出∠BAC=∠C,∠C=∠D,得出∠BAC=∠D,再由公共角∠ABE=∠DBA,即可得出△ABE∽△DBA,求出AB长,由勾股定理可求出AD长,则⊙O半径可求出.
(1)证明:∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠BAD+∠D=90°,
∵∠BAF=∠C,∠C=∠D,
∴∠BAF=∠D,
∴∠BAD+∠BAF=90°,
即∠FAD=90°,
∴AF⊥AD,
∴AF是⊙O的切线;
(2)解:∵AB=BC,
∴![]() ,
,
∴∠BAC=∠C,
∵∠C=∠D,
∴∠BAC=∠D,即∠BAE=∠D,
又∵∠ABE=∠DBA,
∴△ABE∽△DBA;
∴![]() ,
,
∴AB2=BDBE,
∵AB=BC=2![]() ,BE=4,
,BE=4,
∴BD=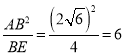 ,
,
∴AD![]() ,
,
∴⊙O半径r=![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
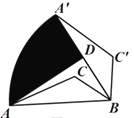
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把如图1所示的菱形称为基本图形,将此基本图形不断复制并平移,使得相邻两个基本图形的一个顶点与对称中心重合,得到的所有菱形都称为基本图形的特征图形,显然图2中有3个特征图形.

(1)观察以上图形并完成如表:
根据表中规律猜想,图n(n≥2)中特征图形的个数为 .(用含n的式子表示)
图形名称 | 基本图形的个数 | 特征图形的个数 |
图1 | 1 | 1 |
图2 | 2 | 3 |
图3 | 3 | 7 |
图4 | 4 | |
…… | …… | …… |
(2)若基本图形的面积为2,则图2中小特征图形的面积是 ;图2020中所有特征图形的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=![]() (x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=
(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=![]() ,则k=_____.
,则k=_____.
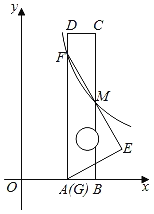
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
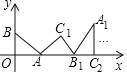
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
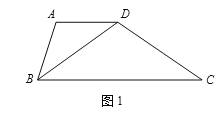
【题目】我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:
求证:
证明:
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中,作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)
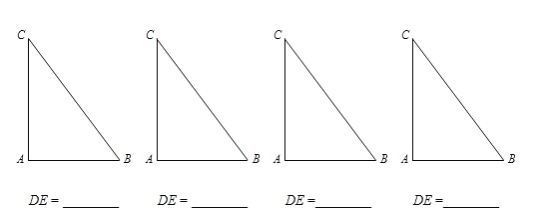
查看答案和解析>>
科目:初中数学 来源: 题型:
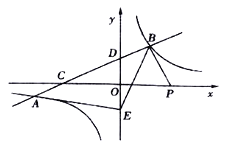
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴、
轴、![]() 轴的交点分别为点
轴的交点分别为点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是
是![]() 轴上一个动点.
轴上一个动点.
(1)填空:①![]() ,
,![]() ;
;
②B点的坐标是 .
(2)若![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察以下等式:
第1个等式:23-22=13+2×1+1;
第2个等式:33-32=23+3×2+22;
第3个等式:43-42=33+4×3+32;
……
按照以上规律,解决下列问题:
(1)写出第4个等式:__________________;
(2)写出你猜想的第n个等式(用含n的等式表示),并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com