
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】
(1)
解:由OH=3,tan∠AOH= ![]() ,得
,得
AH=4.即A(﹣4,3).
由勾股定理,得
AO= ![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)
解:将A点坐标代入y= ![]() (k≠0),得
(k≠0),得
k=﹣4×3=﹣12,
反比例函数的解析式为y= ![]() ;
;
当y=﹣2时,﹣2= ![]() ,解得x=6,即B(6,﹣2).
,解得x=6,即B(6,﹣2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得 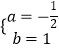 ,
,
一次函数的解析式为y=﹣ ![]() x+1.
x+1.
【解析】(1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;(2)根据待定系数法,可得函数解析式.
【考点精析】解答此题的关键在于理解反比例函数的概念的相关知识,掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数,以及对反比例函数的图象的理解,了解反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】已知,在同一直角坐标系中,反比例函数y= ![]() 与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
(1)求m、c的值;
(2)求二次函数图象的对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°, D是直线AB上的点,AD=BC ,过点A作AF⊥AB,并截取AF=DB ,连接DC、DF、CF ,判断△CDF的形状并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD与矩形EFGO在平面直角坐标系中,点B的坐标为(﹣4,4),点F的坐标为(2,1),若矩形ABCD和矩形EFGO是位似图形,点P(点P在线段GC上)是位似中心,则点P的坐标为( ) 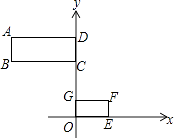
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An﹣1Cn﹣1=An﹣1An.
记∠BA1A=∠1,∠C1A2A1=∠2,……,以此类推. 若∠B=30°,则∠n=_________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小铭和小雨在学习过程中有如下一段对话:
小铭:“我知道一般当m≠n时,![]() ≠
≠![]() .可是我见到有这样一个神奇的等式:
.可是我见到有这样一个神奇的等式:
![]() =
=![]() (其中a,b为任意实数,且b≠0).你相信它成立吗?”
(其中a,b为任意实数,且b≠0).你相信它成立吗?”
小雨:“我可以先给a,b取几组特殊值验证一下看看.”
完成下列任务:
(1)请选择两组你喜欢的、合适的a,b的值,分别代入阅读材料中的等式,写出代入后得到的具体等式并验证它们是否成立(在相应方框内打勾);
① 当a= ,b= 时,等式 (□成立;□不成立);
② 当a= ,b= 时,等式 (□成立;□不成立).
(2)对于任意实数a,b(b≠0),通过计算说明![]() =
=![]() 是否成立.
是否成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com