
【题目】如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,![]() ≈1.7).
≈1.7).
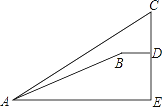
【答案】大树CD的高度约为6.6米.
【解析】
作BF⊥AE于F,则FE=BD=6.4米,DE=BF,设BF=x米,则AF=AF=![]() x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=8米,AF≈13.6米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=8米,AF≈13.6米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
作BF⊥AE于F,如图所示:

则FE=BD=6.4米,DE=BF,
∵斜坡AB的坡角为30°,
∴AF=![]() BF,
BF,
设BF=x米,则AF=![]() x米,
x米,
在Rt△ABF中,由勾股定理得:x2+(![]() x)2=162 ,
x)2=162 ,
解得:x=8,
∴DE=BF=8米,AF≈13.6米,
∴AE=AF+FE=20米,
在Rt△ACE中,CE=AEtan36°≈20×0.73=14.6米,
∴CD=CE﹣DE=14.6﹣8=6.6米.
故大树CD的高度约为6.6米.


科目:初中数学 来源: 题型:
【题目】如图,D,E,F分别是△ABC各边的中点,下列说法中错误的是( )
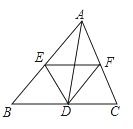
A. △ABC与△DEF是相似形 B. △ABC与△AEF是位似图形 C. EF与AD互相平分 D. AD平分∠BAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
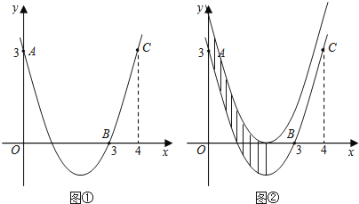
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(![]() +1)EH;③
+1)EH;③![]() =
=![]() . 其中正确的是( )
. 其中正确的是( )
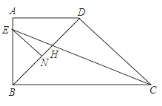
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

查看答案和解析>>
科目:初中数学 来源: 题型:
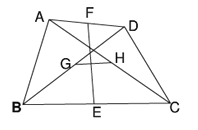
【题目】已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.
①求证:EF与GH互相平分;
②当四边形ABCD的边满足____________条件时,EF⊥GH.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四个半圆彼此相外切,它们的圆心都在x轴的正半轴上并且与直线y=![]() x相切,设半圆C1、C2、C3、C4的半径分别是r1、r2、r3、r4 , 则当r1=1时,r4=( )
x相切,设半圆C1、C2、C3、C4的半径分别是r1、r2、r3、r4 , 则当r1=1时,r4=( )
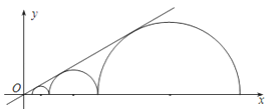
A. 3 B. 32 C. 33 D. 34
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com