
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
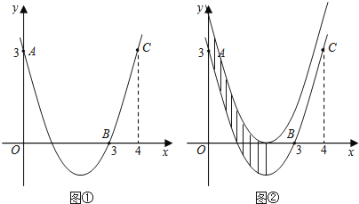
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
【答案】解:(1)∵抛物线![]() 经过点A(0,3),B(3,0),C(4,3),
经过点A(0,3),B(3,0),C(4,3),
∴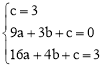 ,解得
,解得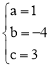 。
。
∴抛物线的函数表达式为![]() 。
。
(2)∵![]() ,
,
∴抛物线的顶点坐标为(2,﹣1),对称轴为直线x=2。
(3)如图,∵抛物线的顶点坐标为(2,﹣1),∴PP′=1。
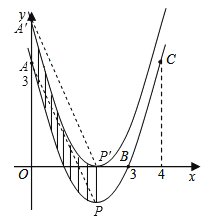
又由平移的性质知,阴影部分的面积等于平行四边形A′APP′的面积,
而平行四边形A′APP′的面积=1×2=2。
∴阴影部分的面积=2。
【解析】
试题分析:(1)把点A、B、C代入抛物线解析式![]() 利用待定系数法求解即可。
利用待定系数法求解即可。
(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可。
(3)根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解。


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
, ![]() .且点
.且点![]() 横坐标是点
横坐标是点![]() 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
(2)设点![]() 横坐标为
横坐标为![]() ,
, ![]() 面积为
面积为![]() ,
,
求![]() 与
与![]() 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
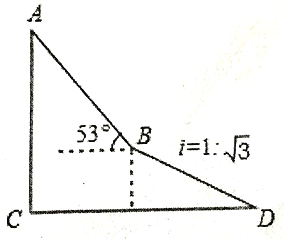
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53![]() ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53![]() =
=![]() , cos53
, cos53![]() =
=![]() , tan53
, tan53![]() =
=![]() ,
, ![]() ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,在第一象限内有一动点
,在第一象限内有一动点![]() 在反比例函数
在反比例函数![]() 上,由点
上,由点![]() 向
向![]() 轴,
轴,![]() 轴所作的垂线
轴所作的垂线![]() ,
,![]() (垂足为
(垂足为![]() ,
,![]() )分别与直线
)分别与直线![]() 相交于点
相交于点![]() ,点
,点![]() ,当点
,当点![]() 运动时,矩形
运动时,矩形![]() 的面积为定值
的面积为定值![]() .
.

(1)求![]() 的度数;
的度数;
(2)求反比例函数解析式.
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com