【题目】如图，直线
与坐标轴分别交于点
，与直线
交于点
是线段
上的动点，连接
，若
是等腰三角形，则
的长为___________．
【答案】2或
或4
【解析】
先求出直线
与直线
交点C的坐标，若使
是等腰三角形，分三种情况讨论，即OQ=CQ或OC=OQ或OC=CQ，在直角三角形中利用勾股定理，根据等腰三角形的性质即可求出OQ．
①如图，当OQ=CQ时，过点C作CE⊥OA于点E，
直线与直线交于点C，
得x=2，
y=x=2
∴C(2,2)
设OQ=CQ=x，QE=2-x
在Rt△CEQ中
解得x=2
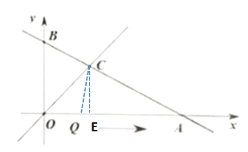
②当OC=OQ时，过点C作CE⊥OA于点E，C(2,2)
在Rt△CEO中， 
OC=
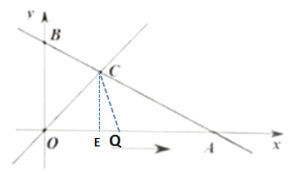
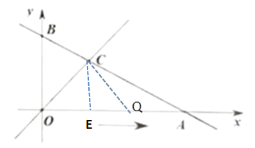
③当OC=CQ时， 过点C作CE⊥OA于点E
∵OC=CQ
∴OE=EQ=2
∴OQ=2OE=4
综上所示，若是等腰三角形，OQ的长为2或或4
故答案为：2或或4
小题狂做系列答案科目：初中数学 来源： 题型：
【题目】如下图，搭一个正方形需要4根火柴棒，搭2个正方形需要7根火柴棒，搭3个正方形需要10根火柴棒．
……
(1)若搭5个这样的正方形，这需要 根火柴棒；
(2)若搭n个这样的正方形，这需要 根火柴棒；
(3)若现在有2018根火柴棒，要搭700个这样的正方形，至少还需要火柴多少根？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连结OD、OE、OC，对于下列结论：
①AD+BC=CD；②∠DOC=90°；③S梯形ABCD=
CDOA；④
．
其中结论正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【1】如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段 .
【1】在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由. 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
【1】如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由. 若此时AB＝3，BD＝
，求BC的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有理数a、b在数轴上的对应点如图所示
(1) 填空：（填“＜”、“＞”或“＝”）
a_________0；b_________0；|a＋b|_________|a|＋|b|
(2) 用“＜”将a、b、－b、
、0连接起来
(3) 化简：|a＋b|－|b＋1|－|a－1|＝______________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，把△ABC绕AC边的中点M旋转后得△DEF，若直角顶点F恰好落在AB边上，且DE边交AB边于点G，若AC=4，BC=3，则AG的长为( )
A.
B.
C.
D.1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，已知抛物线
经过点A（0，3），B（3，0），C（4，3）．
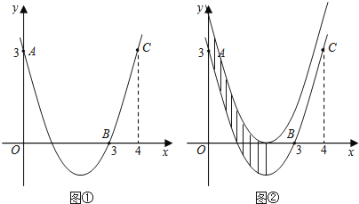
（1）求抛物线的函数表达式；
（2）求抛物线的顶点坐标和对称轴；
（3）把抛物线向上平移，使得顶点落在x轴上，直接写出两条抛物线、对称轴和y轴围成的图形的面积S（图②中阴影部分）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
