
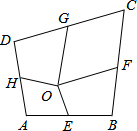
 如图所示,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形形内一点,若
如图所示,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形形内一点,若分析 连接OC,OB,OA,OD,易证S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,S△OAE=S△OBE,所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,所以可以求出S四边形DHOG.
解答 解:连接OC,OB,OA,OD,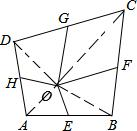
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,所以S△OAE=S△OBE,
同理可证,S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,
∵S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,
∴3+5=4+S四边形DHOG,
解得S四边形DHOG=4.
点评 此题主要考查了三角形面积,解决本题的关键将各个四边形划分,充分利用给出的中点这个条件,证得三角形的面积相等,进而证得结论.


科目:初中数学 来源: 题型:解答题
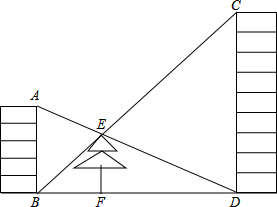 如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.
如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
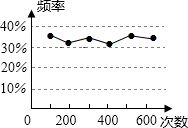 小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )| A. | 掷一枚质地均匀的硬币,正面朝上的概率 | |
| B. | 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率 | |
| C. | 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率 | |
| D. | 任意买一张电影票,座位号是2的倍数的概率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | ab<1 | C. | $\frac{a}{b}$<1 | D. | $\frac{a}{b}$>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | D. | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}$-$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
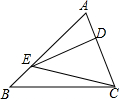 如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )
如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com