
【题目】(1)如图 1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 的直线分别交
的直线分别交![]() 于点
于点![]() 若平行四边形
若平行四边形![]() 的面积是 8,则四边形
的面积是 8,则四边形![]() 的面积是___________ .
的面积是___________ .
(2)如图 2,在菱形![]() 中,对角线相交于点 O,过点 O 的直线分别交
中,对角线相交于点 O,过点 O 的直线分别交![]() 于点
于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)如图 3,在![]() 中,
中,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,若
,若![]() ,则
,则![]() 的面积是____________ .
的面积是____________ .
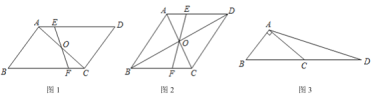
【答案】(1)4;(2)![]() ;(3)3
;(3)3
【解析】
(1)首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
(2)根据菱形的性质得到AD∥BC,AO=CO=![]() AC=2.5,BO=
AC=2.5,BO=![]() BD=5,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
BD=5,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
(3)延长AC到E使CE=AC=3,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到 ![]() ,即可得到结论.
,即可得到结论.
(1)∵四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
在△AOE 和△COF 中
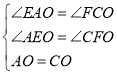
![]()
![]()
(2)∵四边形![]() 是菱形,
是菱形,
![]()
![]()
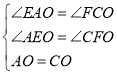
![]()
![]()
![]()
(3)如图,延长![]() 到 E 使
到 E 使![]() ,连结 DE,
,连结 DE,
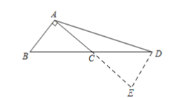
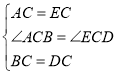
![]()
![]() ,
,
∵![]() ,
,
∴![]()
∴![]()
![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与y轴交于点C.
(1)试用含m的代数式表示抛物线的顶点坐标;
(2)将抛物线y=x2﹣2mx+m2﹣1沿直线y=﹣1翻折,得到的新抛物线与y轴交于点D.若m>0,CD=8,求m的值;
(3)已知A(2k,0),B(0,k),在(2)的条件下,当线段AB与抛物线y=x2﹣2mx+m2﹣1只有一个公共点时,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发:
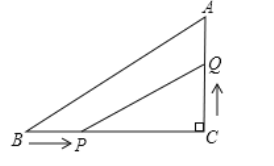
(1)经过多少秒后,△CPQ的面积为8cm?
(2)经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④![]() 其中,正确的 是( )
其中,正确的 是( )

A.只有①②B.只有①②③C.只有③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
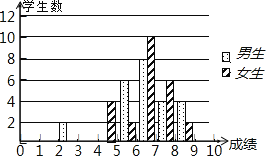
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C(![]() ,0)作CD交AB于D,交
,0)作CD交AB于D,交![]() 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.

(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com