
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
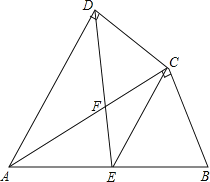
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
【答案】解:(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB。
∵∠ADC=∠ACB=90°,∴△ADC∽△ACB。
∴![]() ,即AC2=ABAD。
,即AC2=ABAD。
(2)证明:∵E为AB的中点,∴CE=![]() AB=AE。∴∠EAC=∠ECA。
AB=AE。∴∠EAC=∠ECA。
∵∠DAC=∠CAB,∴∠DAC=∠ECA。∴CE∥AD。
(3)∵CE∥AD,∴△AFD∽△CFE,∴![]() 。
。
∵CE=![]() AB,∴CE=
AB,∴CE=![]() ×6=3。
×6=3。
∵AD=4,∴![]() 。∴
。∴![]() 。
。
【解析】(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD。
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,从而可证得∠DAC=∠ECA,得到CE∥AD。
AB=AE,从而可证得∠DAC=∠ECA,得到CE∥AD。
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值,从而得到
的值,从而得到![]() 的值。
的值。


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
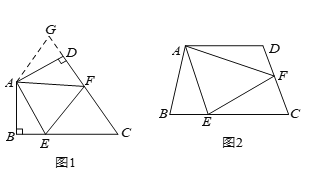
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图像如图所示.根据图像解答下列问题:
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
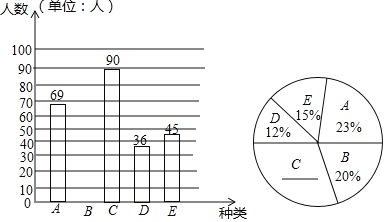
【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市深入贯彻党中央决策部署,高水平建设郑州大都市区,经济实现了持续平稳健康发展.根据2013-2017年郑州市生产总值(单位:亿元)统计图所提供的信息,下列判断一定正确的是( )

A.2014年比2013年的生产总值增加了1000亿元
B.2014-2015年与2016-2017年的生产总值上升率相同
C.预计2018年的生产总值为10146.4亿元
D.2013-2017年生产总值逐年增长,2017年的生产总值达到9130.2亿元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com