
分析 (1)求出方程ax2=b的根,得出方程m+1+2m-4=0,求出即可;
(2)根据(1)中求出的x=$±\sqrt{\frac{b}{a}}$得出$\frac{b}{a}$=(±2)2,求出即可.
解答 解:(1)ax2=b,
x2=$\frac{b}{a}$,
x=$±\sqrt{\frac{b}{a}}$,
即方程的两根互为相反数,
∵一元二次方程ax2=b(ab>0)的两根分别为m+1与2m-4.
∴m+1+2m-4=0,
解得:m=1;
(2)当m=1时,m+1=2,2m-4=-2,
∵x=±$\frac{b}{a}$,一元二次方程ax2=b(ab>0)的两根分别为m+1与2m-4,
∴$\frac{b}{a}$=(±2)2=4.
点评 本题考查了解一元二次方程和相反数,能求出关于m的方程是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
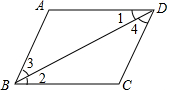 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )| A. | 因为AD∥BC,所以∠3=∠4 | B. | 因为AB∥CD,所以∠ABC+∠C=180° | ||
| C. | 因为∠1=∠2,所以AD∥BC | D. | 因为∠A+∠ADC=180°,所以AB∥CD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 载客量(人/辆) | 40 | 20 |
| 租金(元/辆) | 200 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
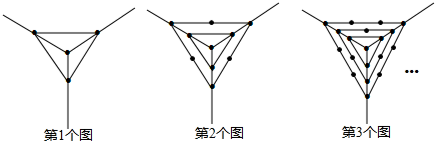
| A. | 38 | B. | 46 | C. | 61 | D. | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com