
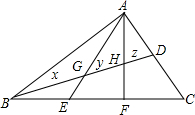
 如图,D是AC的中点,E,F是BC的三等分点,设BG=x,GH=y,HD=z,则x:y:z=5:3:2.
如图,D是AC的中点,E,F是BC的三等分点,设BG=x,GH=y,HD=z,则x:y:z=5:3:2. 分析 作DM∥BC交AE于M,交AF于N,如图,根据平行线分线段成比例定理,由DN∥CF得$\frac{DN}{CF}$=$\frac{AD}{AC}$=$\frac{1}{2}$,由DN∥BF得$\frac{DH}{BH}$=$\frac{DN}{BF}$,于是有$\frac{DN}{2CF}$=$\frac{z}{x+y}$=$\frac{1}{4}$,则x+y=4z,同样方法可得x=y+z,然后解方程组得到x=$\frac{5}{2}$z,y=$\frac{3}{2}$z,
最后计算x、y和z的比值.
解答 解:作DM∥BC交AE于M,交AF于N,如图,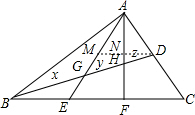
∵DN∥CF,
∴$\frac{DN}{CF}$=$\frac{AD}{AC}$=$\frac{1}{2}$,
∵DN∥BF,
∴$\frac{DH}{BH}$=$\frac{DN}{BF}$,
而BF=2CF,
∴$\frac{DN}{2CF}$=$\frac{z}{x+y}$=$\frac{1}{4}$,
∴x+y=4z①,
∵DM∥CE,
∴$\frac{DM}{CE}$=$\frac{AD}{AC}$=$\frac{1}{2}$,
∵DM∥BE,
∴$\frac{DM}{BE}$=$\frac{DG}{BG}$,
而BE=$\frac{1}{2}$CE,
∴$\frac{DE}{\frac{1}{2}CE}$=$\frac{y+z}{x}$=1,
∴x=y+z②,
由①②得x=$\frac{5}{2}$z,y=$\frac{3}{2}$z,
∴x:y:z=$\frac{5}{2}$z:$\frac{3}{2}$z:z=5:3:2.
故答案为5:3:2.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com