
【题目】平面内的两条直线有相交和平行两种位置关系 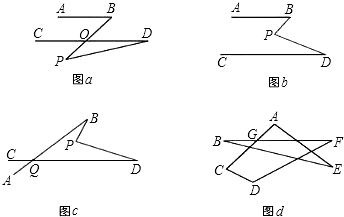
(1)已知AB平行于CD,如a图,当点P在AB、CD外部时,∠BPD+∠D=∠B即∠BPD=∠B﹣∠D,为什么?请说明理由.如b图,将点P移动到AB、CD内部,以上结论是否仍然成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
【答案】
(1)解:①∵AB∥CD,
∴∠B=∠COP,
∵∠COP=∠BPD+∠D,
∴∠B=∠BPD+∠D,
即:∠BPD=∠B﹣∠D,
②不成立,
结论:∠BPD=∠B+∠D,
理由:如图b,

过点P作PG∥AB,
∴∠B=∠BPG,
∵PG∥AB,CD∥AB,
∴PG∥CD,
∴∠DPG=∠D,
∴∠BPD=∠BPG+∠DPG=∠B+∠D
(2)解:结论:∠DPQ=∠B+∠BQD+∠D,
理由:如图c,

连接QP并延长,
∵∠BP∠G是△BPQ的外角,
∴∠BPG=∠B+∠BQP,
同理:∠DPG=∠D+∠DQP,
∴∠BPD=∠BPG+∠DPG=∠B+∠BQP+∠DQP+∠D=∠B+∠BQD+∠D
(3)解:如图d,

∵∠DHM是△BFH的外角,
∴∠DHM=∠B+∠F,
同理:∠CMH=∠A+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠DHM+∠CMH+∠C+∠D=360°
【解析】(1)①利用平行线的性质和三角形的外角即可;②利用平行线的特点作出平行线,再利用平行线的性质即可;(2)利用三角形的外角等于与它不相邻的两内角的和即可;(3)利用三角形的外角的性质把角转化到四边形CDHM中,用四边形的内角和即可.
【考点精析】掌握平行线的性质和旋转的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=![]() 或
或![]() .
.
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司收费标准如下:每月每户用水不超过8吨的部分按0.5元/吨收费;超过8吨而不超过20吨的部分按1元/吨收费;超过20吨的部分按1.6元/吨收费.小明家12月份缴水费24元,则他家该月用水( )吨.
A. 25 B. 30 C. 48 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③b2+8a>4ac;④abc>0,其中正确的有( ).
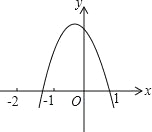
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,该公司每月的投递总件数的平均增长率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题: 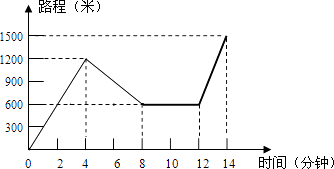
(1)小红家到学校的路程是米,小红在商店停留了分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示) 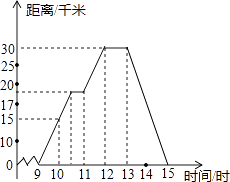
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com