
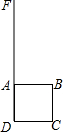
 如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢?
如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢? 分析 结合图形,发现:如果绳长是6m,这头牛在草地上的最大活动区域的面积是圆心角是90°,半径是6m的扇形面积与圆心角是90°,半径是3米的扇形面积的和.
如果绳长是7m,这头牛在草地上的最大活动区域的面积是圆心角是90°,半径是7m的扇形面积与圆心角是90°,半径是4米的扇形面积还有圆心角是90°,半径是1米的扇形面积的和.
解答 解:当绳长为6m时,如图: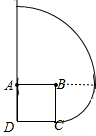
这头牛在草地上的最大活动区域的面积=$\frac{90π×{6}^{2}}{360}$+$\frac{90π×{3}^{2}}{360}$=$\frac{45}{4}$πm2.
故当绳长为6m时,这头牛最多能吃掉面积为$\frac{45}{4}$πm2的草地;
当绳长为7m时,如图: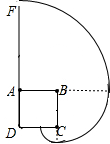
这头牛在草地上的最大活动区域的面积=$\frac{90π×{7}^{2}}{360}$+$\frac{90π×{4}^{2}}{360}$+$\frac{90π×{1}^{2}}{360}$=$\frac{33}{2}$πm2.
故当绳长为7m时,这头牛最多能吃掉面积为$\frac{33}{2}$πm2的草地.
点评 本题考查了扇形面积的计算,画出示意图是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com