
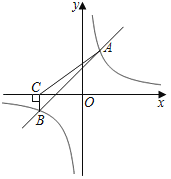
【题目】如图,一次函数y=kx+1与反比例函数y=![]() 的图象相交于A(2,3),B两点.
的图象相交于A(2,3),B两点.
(1)求k、m的值和B点坐标;
(2)过点B作BC⊥x轴于C,连接AC,将△ABC沿x轴向右平移,对应得到△A'B'C',当反比例函数图象经过A'C'的中点M时,求△MAC的面积.
【答案】(1)m=6,k=1,点B的坐标为(﹣3,﹣2);(2)![]() .
.
【解析】
(1)将点A分别代入即可求出k与m的值,再将两个函数解析式联立成方程组即可求出点B的坐标;
(2)设△ABC向右平移了m个单位,将点点M(m﹣![]() ,
,![]() )代入y=
)代入y=![]() 中求出点M的坐标,过点A作y轴的平行线交CM于点H,利用直线CM求出点H,即可求出△MAC的面积.
中求出点M的坐标,过点A作y轴的平行线交CM于点H,利用直线CM求出点H,即可求出△MAC的面积.
解:(1)∵点A(2,3)在y=![]() 的图象上,
的图象上,
∴m=6,
∴反比例函数的解析式为:y=![]() ①,
①,
将点A的坐标代入一次函数表达式得:3=2k+1,
解得:k=1,
故一次函数表达式为:y=x+1②,
联立①②得 ,解得:
,解得:![]() 或
或![]() ,
,
故点B的坐标为(﹣3,﹣2);
(2)如图,设△ABC向右平移了m个单位,则点A′、C′的坐标分别为(2+m,3)、(﹣3+m,0),
则点M(m﹣![]() ,
,![]() ),
),
将点M的坐标代入①式并解得:m=![]() ,
,
故点M(4,![]() ),
),
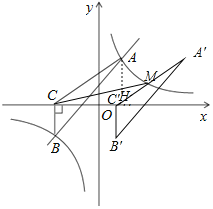
过点A作y轴的平行线交CM于点H,
设直线CM的解析式为y=k1x+b,
∴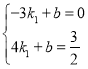 ,解得
,解得 ,
,
∴直线CM的表达式为:![]() ,
,
当x=2时,y=![]() ,故点H(2,
,故点H(2,![]() ),
),
△MAC的面积S=S△AHC+S△AHM=![]() ×AH×(xM﹣xC)=
×AH×(xM﹣xC)=![]() (3﹣
(3﹣![]() )×(4+3)=
)×(4+3)=![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=![]() 的图象上,OA=5,OC=1,则△ODE的面积为( )
的图象上,OA=5,OC=1,则△ODE的面积为( )
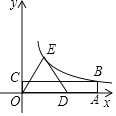
A.2.5B.5C.7.5D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.

根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A. 李飞或刘亮 B. 李飞 C. 刘亮 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:

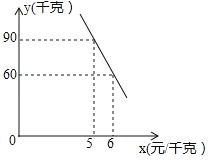
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0.1cm;参考数据sin70°≈0. 94,cos70°≈0.34,sin20°≈0.34,cos20°≈0.94)
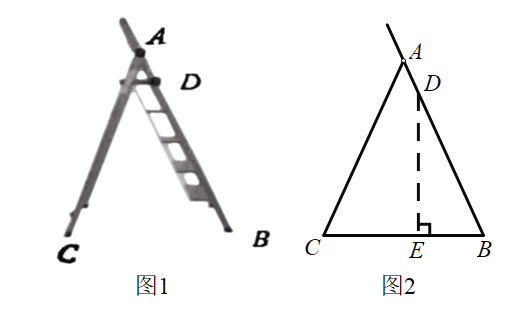
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B为直线y=x上的两点,过A、B两点分别作y轴的平行线交双曲线![]() (x>0)于点C、D两点.若BD=2AC,则4OC2﹣OD2的值为( )
(x>0)于点C、D两点.若BD=2AC,则4OC2﹣OD2的值为( )

A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
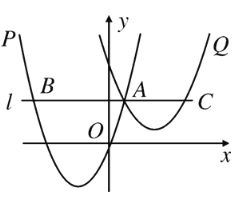
【题目】如图,抛物线P:y1=a(x+2)2-3与抛物线Q:y2=![]() (x-t)2+1在同一个坐标系中(其中a、t均为常数,且t>0),已知抛物线P过点A(1,3),过点A作直线l∥x轴,交抛物线P于点B.
(x-t)2+1在同一个坐标系中(其中a、t均为常数,且t>0),已知抛物线P过点A(1,3),过点A作直线l∥x轴,交抛物线P于点B.
(1)a=________,点B的坐标是________;
(2)当抛物线Q经过点A时.
①求抛物线Q的解析式;
②设直线l与抛物线Q的另一交点记作C,求![]() 的值;
的值;
(3)若抛物线Q与线段AB总有唯一的交点,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com