
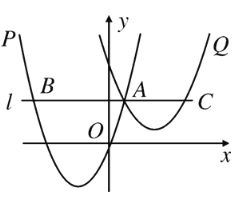
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпPЃКy1ЃНaЃЈxЃЋ2ЃЉ2Ѓ3гыХзЮяЯпQЃКy2ЃН![]() ЃЈxЃtЃЉ2ЃЋ1дкЭЌвЛИізјБъЯЕжаЃЈЦфжаaЁЂtОљЮЊГЃЪ§ЃЌЧвtЃО0ЃЉЃЌвбжЊХзЮяЯпPЙ§ЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїжБЯпlЁЮxжсЃЌНЛХзЮяЯпPгкЕуBЃЎ
ЃЈxЃtЃЉ2ЃЋ1дкЭЌвЛИізјБъЯЕжаЃЈЦфжаaЁЂtОљЮЊГЃЪ§ЃЌЧвtЃО0ЃЉЃЌвбжЊХзЮяЯпPЙ§ЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїжБЯпlЁЮxжсЃЌНЛХзЮяЯпPгкЕуBЃЎ
ЃЈ1ЃЉaЃН________ЃЌЕуBЕФзјБъЪЧ________ЃЛ
ЃЈ2ЃЉЕБХзЮяЯпQОЙ§ЕуAЪБЃЎ
ЂйЧѓХзЮяЯпQЕФНтЮіЪНЃЛ
ЂкЩшжБЯпlгыХзЮяЯпQЕФСэвЛНЛЕуМЧзїCЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєХзЮяЯпQгыЯпЖЮABзмгаЮЈвЛЕФНЛЕуЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ ![]() ЃЛЃЈЃ5ЃЌ3ЃЉЃЛЃЈ2ЃЉЂйХзЮяЯпQЕФНтЮіЪНЮЊЃКy2ЃН
ЃЛЃЈЃ5ЃЌ3ЃЉЃЛЃЈ2ЃЉЂйХзЮяЯпQЕФНтЮіЪНЮЊЃКy2ЃН ![]() ЃЈxЃ3ЃЉ2ЃЋ1ЃЛЂк
ЃЈxЃ3ЃЉ2ЃЋ1ЃЛЂк![]() ЃН
ЃН![]() ЃЛЃЈ3ЃЉ0ЃМt
ЃЛЃЈ3ЃЉ0ЃМt![]() 3ЃЎ
3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпPЕФНтЮіЪНЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЂйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпQЕФНтЮіЪНЃЌМДПЩЕУГіНсТлЃЛЂкЯШЧѓГіACЃЌABМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉРћгУЦНвЦЕФЬиЕуКЭABЃЌACЕФГЄМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпPЃКy1ЃНaЃЈxЃЋ2ЃЉ2Ѓ3Й§ЕуAЃЈ1ЃЌ3ЃЉЃЌ
Ёр9aЃ3ЃН3ЃЌ
ЁрaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпPЃКy1ЃН ![]() ЃЈxЃЋ2ЃЉ2Ѓ3ЃЌ
ЃЈxЃЋ2ЃЉ2Ѓ3ЃЌ
Ёп![]()
![]() xжсЃЌ
xжсЃЌ
ЁрЕуBЕФзнзјБъЮЊ3ЃЌ
Ёр3ЃН ![]() ЃЈxЃЋ2ЃЉ2Ѓ3ЃЌ
ЃЈxЃЋ2ЃЉ2Ѓ3ЃЌ
Ёрx1ЃН1ЃЈЕуAЕФКсзјБъЃЉЃЌx2ЃНЃ5ЃЌ
ЁрBЃЈЃ5ЃЌ3ЃЉЃЎ
ЃЈ2ЃЉЂйЁпХзЮяЯпQЃКy2ЃН![]() ЃЈxЃtЃЉ2ЃЋ1Й§ЕуAЃЈ1ЃЌ3ЃЉЃЌ
ЃЈxЃtЃЉ2ЃЋ1Й§ЕуAЃЈ1ЃЌ3ЃЉЃЌ
Ёр![]() ЃЈ1ЃtЃЉ2ЃЋ1ЃН3ЃЌ
ЃЈ1ЃtЃЉ2ЃЋ1ЃН3ЃЌ
Ёрt1ЃНЃ1ЃЈЩсШЅЃЉЃЌt2ЃН3ЃЌ
ЁрХзЮяЯпQЕФНтЮіЪНЮЊЃКy2ЃН ![]() ЃЈxЃ3ЃЉ2ЃЋ1ЃЛ
ЃЈxЃ3ЃЉ2ЃЋ1ЃЛ
Ёп![]()
![]() xжсЃЌ
xжсЃЌ
ЁрЕуCЕФзнзјБъЮЊ3ЃЌ
Ёр3ЃН![]() ЃЈxЃ3ЃЉ2ЃЋ1ЃЌ
ЃЈxЃ3ЃЉ2ЃЋ1ЃЌ
Ёрx1ЃН1ЃЈЕуAЕФКсзјБъЃЉЃЌx2ЃН5ЃЌ
ЁрCЃЈ5ЃЌ3ЃЉЃЌ
ЁрACЃН5Ѓ1ЃН4ЃЌ
гЩЃЈ1ЃЉжЊЃЌBЃЈЃ5ЃЌ3ЃЉЃЌ
ЁрABЃН1ЃЃЈЃ5ЃЉЃН6ЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпХзЮяЯпQЃКy2ЃН![]() ЃЈxЃtЃЉ2ЃЋ1
ЃЈxЃtЃЉ2ЃЋ1
ЁрХзЮяЯпQЕФПЊПкДѓаЁвЛЖЈЃЌЖЅЕузјБъЕФзнзјБъЪЧ1вВЪЧЖЈжЕЃЌ
ЁрХзЮяЯпQжЛЪЧзѓгввЦЖЏЃЌ
ЕБХзЮяЯпQЯђгвЦНвЦЕФЙ§ГЬжаЃЌЕуAдкХзЮяЯпQЕФзѓВрЪБЃЌХзЮяЯпQКЭЯпЖЮABгавЛИіНЛЕуAЃЌДЫЪБЃЌt=3ЃЌ
гЩЃЈ2ЃЉжЊЃЌAC=4ЃЌНЋХзЮяЯпQЯђзѓЦНвЦ4ИіЕЅЮЛЪБЃЌКЭЯпЖЮABгаСНИіНЛЕуЃЌДЫЖЮЃЌЃ1ЃМt![]() 3ЪБЃЌХзЮяЯпQгыЯпЖЮABгавЛИіНЛЕуЃЌ
3ЪБЃЌХзЮяЯпQгыЯпЖЮABгавЛИіНЛЕуЃЌ
дйМЬајАбХзЮяЯпQЯђзѓвЦЖЏЃЌвЦЖЏЕНЕуBдкХзЮяЯпQЕФзѓВрЪБЃЌДЫЪБЃЌДЫЪБЃЌt=Ѓ3ЃЌ
ЭЌЩЯЃЌХзЮяЯпQгыЯпЖЮABгавЛИіНЛЕуЃЌЃ7![]() tЃМЃ3ЃЌ
tЃМЃ3ЃЌ
ЁпtЃО0ЃЌ
МДЃК0ЃМt![]() 3ЃЌХзЮяЯпQгыЯпЖЮABгавЛИіНЛЕуЃЎ
3ЃЌХзЮяЯпQгыЯпЖЮABгавЛИіНЛЕуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
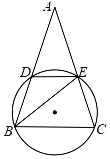
ЁОЬтФПЁПШчЭМЃЌЕШбќЁїABCСНбќABЃЌACЗжБ№НЛЁбOгкЕуDЃЌEЃЌЕуAдкЁбOЭтЃЌЕуBЃЌCдкЁбOЩЯЃЈВЛгыDЃЌEжиКЯЃЉЃЌСЌНсBEЃЌDEЃЎвбжЊЁЯAЃНЁЯEBCЃЌЩш![]() ЃНkЃЈ0ЃМkЃМ1ЃЉЃЎ
ЃНkЃЈ0ЃМkЃМ1ЃЉЃЎ
ЃЈ1ЃЉШєЁЯAЃН50ЁуЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєkЃН![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЩшЁїABCЃЌЁїADEЃЌЁїBECЕФжмГЄЗжБ№ЮЊcЃЌc1ЃЌc2ЃЌЧѓжЄЃК1ЃМ![]() Ём
Ём![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
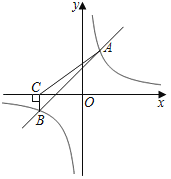
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+1гыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЯрНЛгкAЃЈ2ЃЌ3ЃЉЃЌBСНЕуЃЎ
ЕФЭМЯѓЯрНЛгкAЃЈ2ЃЌ3ЃЉЃЌBСНЕуЃЎ
ЃЈ1ЃЉЧѓkЁЂmЕФжЕКЭBЕузјБъЃЛ
ЃЈ2ЃЉЙ§ЕуBзїBCЁЭxжсгкCЃЌСЌНгACЃЌНЋЁїABCбиxжсЯђгвЦНвЦЃЌЖдгІЕУЕНЁїA'B'C'ЃЌЕБЗДБШР§КЏЪ§ЭМЯѓОЙ§A'C'ЕФжаЕуMЪБЃЌЧѓЁїMACЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭјЕъзЈЪлвЛПюЕчЖЏбРЫЂЃЌЦфГЩБОЮЊ20дЊ/жЇЃЌЯњЪлжаЗЂЯжЃЌИУЩЬЦЗУПЬьЕФЯњЪлСПy(жЇЃЉгыЯњЪлЕЅМлx(дЊ/жЇЃЉжЎМфДцдкШчЭМЫљЪОЕФЙиЯЕЃЎ
(1)ЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
(2)гЩгкКўББЪЁЮфККЪаБЌЗЂСЫаТаЭЙкзДВЁЖОЗЮбзЃЈМђГЦЁАаТЙкЗЮбзЁБЃЉвпЧщЃЌИУЭјЕъЕъжїОіЖЈДгУПЬьЛёЕУЕФРћШѓжаГщГі200дЊОшЯзИјЮфККЃЌЮЊСЫБЃжЄОшПюКѓУПЬьЪЃгрРћШѓВЛЕЭгк550дЊЃЌШчКЮШЗЖЈетПюЕчЖЏбРЫЂЕФЯњЪлЕЅМлЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпlЃКy=Љx+4ЃЌдкжБЯпlЩЯШЁЕуB1ЃЌЙ§B1ЗжБ№ЯђxжсЃЌyжсзїДЙЯпЃЌНЛxжсгкA1ЃЌНЛyжсгкC1ЃЌЪЙЫФБпаЮOA1B1C1ЮЊе§ЗНаЮЃЛдкжБЯпlЩЯШЁЕуB2ЃЌЙ§B2ЗжБ№ЯђxжсЃЌA1B1зїДЙЯпЃЌНЛxжсгкA2ЃЌНЛA1B1гкC2ЃЌЪЙЫФБпаЮA1A2B2C2ЮЊе§ЗНаЮЃЛАДДЫЗНЗЈдкжБЯпlЩЯЫГДЮШЁЕуB3ЃЌB4ЃЌЁЃЌBnЃЌвРДЮзїе§ЗНаЮA2A3B3C3ЃЌA3A4B4C4ЃЌЁЃЌAnЉ1AnBnCnЃЌдђA3ЕФзјБъЮЊ___ЃЌB5ЕФзјБъЮЊ___ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
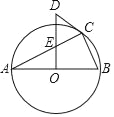
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌЧвABЮЊЁбOЕФжБОЖЃЌODЁЭABЃЌгыACНЛгкЕуEЃЌЁЯDЃН2ЁЯAЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКDEЃНDCЃЛ
ЃЈ3ЃЉШєODЃН5ЃЌCDЃН3ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
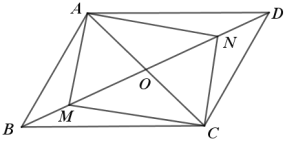
ЁОЬтФПЁПШчЭМЃЌвбжЊЦНааЫФБпаЮABCDЃЎ
ЃЈ1ЃЉШєMЃЌNЪЧBDЩЯСНЕуЃЌЧвBMЃНDNЃЌACЃН2OMЃЌЧѓжЄЃКЫФБпаЮAMCNЪЧОиаЮЃЛ
ЃЈ2ЃЉШєЁЯBADЃН120ЁуЃЌCDЃН4ЃЌABЁЭACЃЌЧѓЦНааЫФБпаЮABCDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
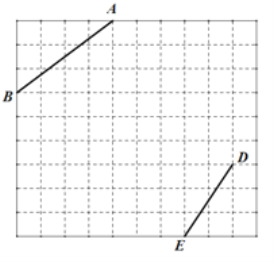
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаУПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ 1ЃЌЯпЖЮ ABЁЂDE ЕФЖЫЕу AЁЂBЁЂDЁЂE ОљдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЎ
ЃЈ1ЃЉдкЭМжаЛвЛИівд AB ЮЊвЛбќЕФЕШбќЁїABCЃЌ Чвtan ABC ![]() ЃЌЕуC дкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЛ
ЃЌЕуC дкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЛ
ЃЈ2ЃЉдкЭМжаЛвЛИівд DE ЮЊБпЕФЦНааЫФБпаЮ DEFGЃЌЧвG 45Ёу ЃЌЕу FЁЂG ОљдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌСЌНг CGЃЌЧыжБНгаДГіЯпЖЮ CG ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЌвдЕуAЮЊдВаФЃЌаЁгкACГЄЮЊАыОЖзїдВЛЁЃЌЗжБ№НЛABЃЌACгкEЃЌFСНЕуЃЌдйЗжБ№вдEЃЌFЮЊдВаФЃЌДѓгк![]() EFГЄЮЊАыОЖзїдВЛЁЃЌСНЬѕдВЛЁНЛгкЕуPЃЌСЌНгAPЃЌНЛCDгкЕуMЃЌШєЁЯACDЃН110ЁуЃЌдђЁЯCMAЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ
EFГЄЮЊАыОЖзїдВЛЁЃЌСНЬѕдВЛЁНЛгкЕуPЃЌСЌНгAPЃЌНЛCDгкЕуMЃЌШєЁЯACDЃН110ЁуЃЌдђЁЯCMAЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ
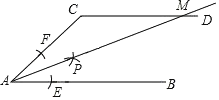
A.30ЁуB.35ЁуC.70ЁуD.45Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com