
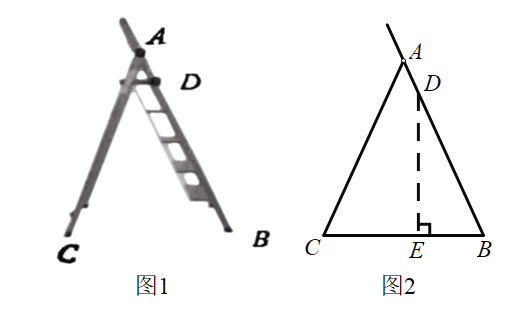
【题目】人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0.1cm;参考数据sin70°≈0. 94,cos70°≈0.34,sin20°≈0.34,cos20°≈0.94)
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
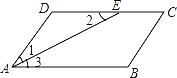
【题目】如图,在ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.
(1)求EC的长.
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班兴趣小组对函数y=﹣x2+2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣3 |
| 0 | 1 | 0 | 1 | 0 |
| ﹣3 | … |
(1)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分;
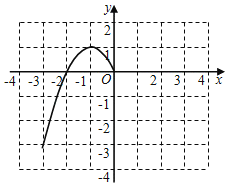
(2)观察函数图象,当y随x增大而减小时,则x的取值范围是
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程﹣x2+2|x|=0有 个实数根;
②方程﹣x2+2|x|=﹣1有 个实数根;
③若关于x的方程﹣x2+2|x|=n有4个实数根,则n的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
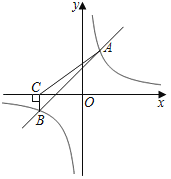
【题目】如图,一次函数y=kx+1与反比例函数y=![]() 的图象相交于A(2,3),B两点.
的图象相交于A(2,3),B两点.
(1)求k、m的值和B点坐标;
(2)过点B作BC⊥x轴于C,连接AC,将△ABC沿x轴向右平移,对应得到△A'B'C',当反比例函数图象经过A'C'的中点M时,求△MAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:m),如果在离水面竖直距离为h(单校:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H—h).
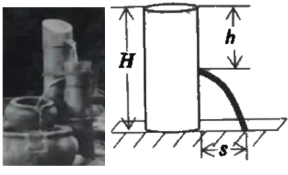
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)求y与x之间的函数关系式.
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?

查看答案和解析>>
科目:初中数学 来源: 题型:
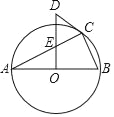
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
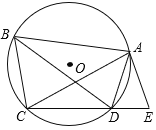
【题目】如图,四边形ABCD内接于⊙O,已知AB=AC,延长CD至点E,使CE=BD,连结AE.
(1)求证:AD平分∠BDE;
(2)若AB∥CD,求证:AE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com