
【题目】某班兴趣小组对函数y=﹣x2+2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣3 |
| 0 | 1 | 0 | 1 | 0 |
| ﹣3 | … |
(1)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分;
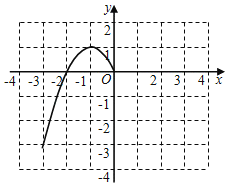
(2)观察函数图象,当y随x增大而减小时,则x的取值范围是
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程﹣x2+2|x|=0有 个实数根;
②方程﹣x2+2|x|=﹣1有 个实数根;
③若关于x的方程﹣x2+2|x|=n有4个实数根,则n的取值范围是 .
【答案】(1)详见解析;(2)﹣1<x<0,x>1;(3)①3,3;②2;③0<n<1
【解析】
(1)根据函数的对称性补充图象如图所示;
(2)观察图象,从左到右下降的图象上点的横坐标x的取值范围即为所求;
(3)①观察图象,即可求解;②函数y=﹣x2+2|x|的图象与直线y=-1的交点个数即为方程﹣x2+2|x|=﹣1实数解得个数;③结合图象,当直线y=n与函数y=﹣x2+2|x|的图象有四个交点时,n范围即为所求.
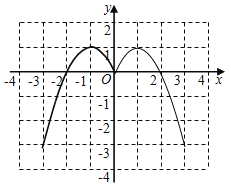
解:(1)补充图象另一部分如下:
(2)从图象看,当y随x增大而减小时,则x的取值范围是:﹣1<x<0,x>1;
故答案是:﹣1<x<0,x>1;
(3)从图象看①函数图象与x轴有3个交点,所以对应方程﹣x2+2|x|=0有3个实数根;
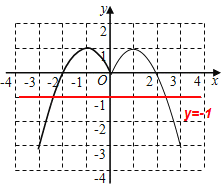
②从图象上看,函数y=﹣x2+2|x|的图象与直线y=-1的交点个数是2个,故方程﹣x2+2|x|=﹣1有2个实数根;
③若关于x的方程﹣x2+2|x|=n有4个实数根,则直线y=n与函数y=﹣x2+2|x|的图象有四个交点时,由图可知,n的取值范围是0<n<1,
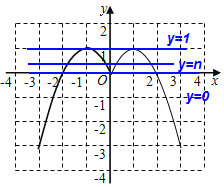
故答案为:3,3;2;0<n<1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2bx+1﹣2b(b为常数).
(1)若点(2,5)在该抛物线上,求b的值;
(2)若该抛物线的顶点坐标是(m,n),求n关于m的函数解析式;
(3)若抛物线与x轴交点之间的距离大于4,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+6与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0<m<6)且垂直于y轴的直线与二次函数y=ax2+c的图象相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直升机的镜头下,观测东营市清风湖A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为300米,点A、B、D在同一条直线上,则A、B两点间的距离为____米.(结果保留根号)
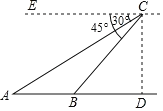
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.

根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A. 李飞或刘亮 B. 李飞 C. 刘亮 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0.1cm;参考数据sin70°≈0. 94,cos70°≈0.34,sin20°≈0.34,cos20°≈0.94)
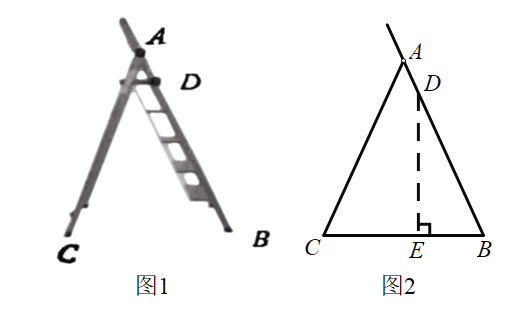
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BD=AB,∠ABD=30°,将平行四边形ABCD绕点A旋转至平行四边形AMNE的位置,使点E落在BD上, ME交AB于点O, 则![]() 的值是( )
的值是( )
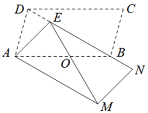
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com