
【题目】一次函数y=kx+6与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0<m<6)且垂直于y轴的直线与二次函数y=ax2+c的图象相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)先将点![]() 代入一次函数的解析式可求出k的值,从而可得一次函数的解析式,再根据二次函数的解析式可得其顶点坐标为
代入一次函数的解析式可求出k的值,从而可得一次函数的解析式,再根据二次函数的解析式可得其顶点坐标为![]() ,然后将其代入一次函数的解析式可求出c的值,最后将点
,然后将其代入一次函数的解析式可求出c的值,最后将点![]() 代入二次函数的解析式可求出a的值;
代入二次函数的解析式可求出a的值;
(2)先由(1)的结论得出二次函数的解析式,再令![]() 可求出点B、C的横坐标,从而可得
可求出点B、C的横坐标,从而可得![]() ,由此可得出W关于m的函数解析式,然后根据二次函数的性质求最小值即可.
,由此可得出W关于m的函数解析式,然后根据二次函数的性质求最小值即可.
(1)由题意,将点![]() 代入一次函数的解析式得:
代入一次函数的解析式得:![]()
解得![]()
则一次函数的解析式为![]()
二次函数![]() 的顶点坐标为
的顶点坐标为![]()
由题意知,![]() 在一次函数
在一次函数![]() 的图象上
的图象上
则![]()
将点![]() 代入二次函数的解析式得:
代入二次函数的解析式得:![]() ,即
,即![]()
解得![]()
综上,![]() ,
,![]() ,
,![]() ;
;
(2)由(1)得,二次函数的解析式为![]()
由题意,可设点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]()
令![]() 得
得![]() ,即
,即![]()
解得![]()
则![]()
![]()
![]()
则![]()
整理得:![]()
![]()
![]() 当
当![]() 时,W随m的增大而减小;当
时,W随m的增大而减小;当![]() 时,W随m的增大而增大
时,W随m的增大而增大
则当![]() 时,W取得最小值,最小值为
时,W取得最小值,最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某街道组织志愿者活动,选派志愿者到小区服务.若每一个小区安排4人,那么还剩下78人;若每个小区安排8人,那么最后一个小区不足8人,但不少于4人.求这个街道共选派了多少名志愿者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:①![]() ;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中错误的个数是( )
;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
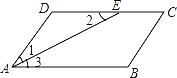
【题目】如图,在ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.
(1)求EC的长.
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
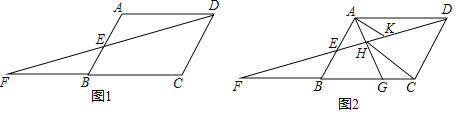
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+1)(x﹣m)(a为非零常数,1<m<2),当x<﹣1时,y随x的增大而增大,说法正确的是( )
A.若图象经过点(0,1),则﹣![]() <a<0
<a<0
B.若x>﹣![]() 时,则y随x的增大而增大
时,则y随x的增大而增大
C.若(﹣2020,y1),(2020,y2)是函数图象上的两点,则y1<y2
D.若图象上两点(![]() ,y1),(
,y1),(![]() +n,y2)对一切正数n,总有y1>y2,则
+n,y2)对一切正数n,总有y1>y2,则![]() ≤m<2
≤m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
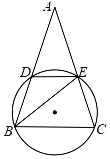
【题目】如图,等腰△ABC两腰AB,AC分别交⊙O于点D,E,点A在⊙O外,点B,C在⊙O上(不与D,E重合),连结BE,DE.已知∠A=∠EBC,设![]() =k(0<k<1).
=k(0<k<1).
(1)若∠A=50°,求![]() 的度数;
的度数;
(2)若k=![]() ,求
,求![]() 的值;
的值;
(3)设△ABC,△ADE,△BEC的周长分别为c,c1,c2,求证:1<![]() ≤
≤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班兴趣小组对函数y=﹣x2+2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣3 |
| 0 | 1 | 0 | 1 | 0 |
| ﹣3 | … |
(1)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分;
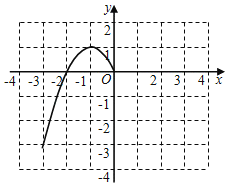
(2)观察函数图象,当y随x增大而减小时,则x的取值范围是
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程﹣x2+2|x|=0有 个实数根;
②方程﹣x2+2|x|=﹣1有 个实数根;
③若关于x的方程﹣x2+2|x|=n有4个实数根,则n的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)求y与x之间的函数关系式.
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com