练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某街道组织志愿者活动，选派志愿者到小区服务．若每一个小区安排4人，那么还剩下78人；若每个小区安排8人，那么最后一个小区不足8人，但不少于4人．求这个街道共选派了多少名志愿者？

    【答案】街道组织的是158名志愿者，分到了20个小区服务

    【解析】

    设该社区共有x个街道，则总人数=街道数×每个街道安排的人数+剩余的人数，即总人数=4x+78；若每个街道安排8个时，则最后一个街道安排的人数=总人数-前几个街道安排的人数，即最后一个街道安排的人数=4x+78-8（x-1）；又知最后一个街道不足8人，但不少于4人，则可得不等式4≤4x+78-8（x-1）＜8；解得x的取值范围，再确定x的值，最后求得总人数．

    解：设共到x个小区，有志愿者（4x+78）人，由题意得

    解得

    根据题意x=20，这时志愿者为158人．

    答：街道组织的是158名志愿者，分到了20个小区服务．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】 为满足社区居民健身的需要，市政府准备采购若干套健身器材免费提供给社区，经考察，劲松公司有两种型号的健身器可供选择.

    （1）劲松公司2015年每套型健身器的售价为万元，经过连续两年降价，2017年每套售价为 万元，求每套型健身器年平均下降率 ；

    （2）2017年市政府经过招标，决定年内采购并安装劲松公司两种型号的健身器材共套，采购专项费总计不超过万元，采购合同规定：每套型健身器售价为万元，每套型健身器售价我 万元.

    ①型健身器最多可购买多少套？

    ②安装完成后，若每套型和型健身器一年的养护费分别是购买价的 和 .市政府计划支出 万元进行养护.问该计划支出能否满足一年的养护需要？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是等边三角形，点D为平面内一点，连接DB、DC，∠BDC＝120°．

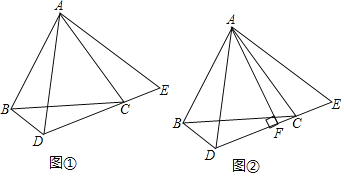
    （1）如图①，当点D在BC下方时，连接AD，延长DC到点E，使CE＝BD，连接AE．

    ①求证：△ABD≌△ACE；

    ②如图②，过点A作AF⊥DE于点F，直接写出线段AF、BD、DC间的数量关系；

    （2）若AB＝2，DC＝6，直接写出点A到直线BD的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．

    （1）求y关于x的函数关系式；（不需要写定义域）

    （2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】新冠疫情初期，医用口罩是紧缺物资．某市为降低因购买口罩造成人群聚集的感染风险，通过APP实名预约，以摇号抽签的方式，由市民到指定门店购买口罩．规定：已中签者在本轮摇号结束前不再参与摇号；若指定门店当日市民购买口罩的平均等待时间超过8分钟，则次日必须增派工作人员．

    （1）据APP数据统计：第一天有386.5万人进行网上预约，此后每天预约新增4万人，且每天有35.5万人中签，若小明第一天没有中签，则他第二天中签的概率是多少？

    （2）该市某区指定A，B两门店每天8:00-22:00时段让中签市民排队购买口罩．图1是A门店某日购买口罩的人数与等待时间的统计图，为了算出A门店某日等待9分钟的人数，小红选择14：00~16：00这个时间段到店进行统计，统计结果见表1，且这个时间段的人数占该店当天等待9分钟人数的．表2是B门店某日购买口罩的人数与等待时间的统计表．请你运用所学的统计知识判断A，B门店次日是否需要增派工作人员．

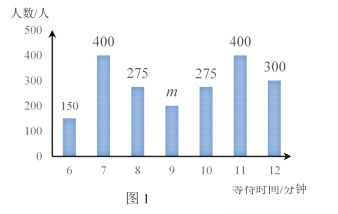
    表1

    时间段

    等待9分钟/人

    14:00~14:30

    10

    14:30~15:00

    20

    15:00~15:30

    15

    15:30~16:00

    5

    表2

    等待时间

    人数/人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）（问题发现）如图1，△ABC和△ADE均为等边三角形，点B，D，E在同一条直线上．填空：①线段BD，CE之间的数量关系为 ；②∠BEC = °．

    　　　　　　　　

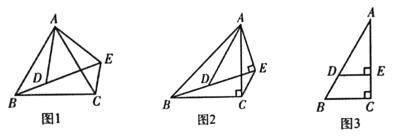
    （2）（类比探究）如图2，△ABC和△ADE均为等腰直角三角形，∠ACB=∠AED=90°，AC=BC，AE=DE，点B，D，E在同一条直线上，请判断线段BD，CE之间的数量关系及∠BEC的度数，并给出证明．

    （3）如图3，在△ABC中，∠ACB=90°，∠A=30°，AB = 5，点D在AB 边上，DE⊥AC于点E，AE = 3，将△ADE绕点A旋转，当DE所在直线经过点B时，CE的长是多少？（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，在平面直角坐标系中，直线y1＝kx+b与x轴交于点A（4，0），与y轴交于点B（0，3），点C是直线y2＝x+5上的一个动点，连接BC，过点C作CD⊥AB于点D．

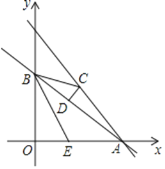
    (1)求直线y1＝kx+b的函数表达式；

    (2)当BC∥x轴时，求BD的长；

    (3)点E在线段OA上，OE＝OA，当点D在第一象限，且△BCD中有一个角等于∠OEB时，请直接写出点C的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=﹣x2+2bx+1﹣2b(b为常数)．

    （1）若点(2，5)在该抛物线上，求b的值；

    （2）若该抛物线的顶点坐标是(m，n)，求n关于m的函数解析式；

    （3）若抛物线与x轴交点之间的距离大于4，求b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y＝kx+6与二次函数y＝ax2+c的图象的一个交点坐标为（1，2），另一个交点是该二次函数图象的顶点．

    （1）求k，a，c的值；

    （2）过点A（0，m）（0＜m＜6）且垂直于y轴的直线与二次函数y＝ax2+c的图象相交于B，C两点，点O为坐标原点，记W＝OA2+BC2，求W关于m的函数解析式，并求W的最小值．

    查看答案和解析>>

    同步练习册答案