
����Ŀ��һ��������ij����ʻ�����У������е�ʣ������y����������ʻ·��x��ǧ�ף�֮����һ�κ�����ϵ���䲿��ͼ����ͼ��ʾ��
��1����y����x�ĺ�����ϵʽ��������Ҫд������
��2����֪�������е�ʣ������Ϊ8��ʱ���������Ὺʼ��ʾ���ͣ��ڴ˴���ʻ�����У���ʻ��500ǧ��ʱ��˾��������ǰ������ļ���վ��30ǧ��·�̣��ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·���Ƕ���ǧ�ף�

���𰸡���1����һ�κ�������ʽΪy=��![]() x+60����2���ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·����10ǧ�ף�
x+60����2���ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·����10ǧ�ף�
��������
��1�����ݺ���ͼ���е���������ô���ϵ�������һ�κ�������ʽ��
��2������һ�κ���ͼ���ϵ�����������������ʣ������Ϊ8��ʱ��ʻ��·�̣�������ô�.
��1�����һ�κ�������ʽΪy=kx+b��
����150��45������0��60������y=kx+b����
![]() ����ã�
����ã�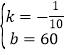 ��
��
���һ�κ�������ʽΪy=��![]() x+60��
x+60��
��2����y=��![]() x+60=8ʱ��
x+60=8ʱ��
���x=520��
����ʻ520ǧ��ʱ�������е�ʣ������Ϊ8����
530��520=10ǧ�ף�
�����е�ʣ������Ϊ8��ʱ���������վ10ǧ����
���ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·����10ǧ�ף�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪С������ABCD�����Ϊ1�������ĸ����ӳ�һ���õ���������A1B1C1D1����������A1B1C1D1�ĸ��߳���ԭ���ӳ�һ���õ�������A2B2C2D2���Դ˽�����ȥ����������A4B4C4D4�����Ϊ_____��������AnBnCnDn�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C�ǡ�O�ϵ����㣬AB��OC��
��1����֤��ACƽ�֡�OAB��
��2������O��OE��AB�ڵ�E����AC�ڵ�P����AB=2����AOE=30�㣬��PE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ�� ![]() �ֱ�x�ᡢy����A��B���㣮
�ֱ�x�ᡢy����A��B���㣮
��1����A��B��������ꣻ
��2����P��ֱ��AB��һ���㣨��P���A���غϣ�����Pʼ�պ�x�����У���ֱ��AB�ཻ��C��D���㣨��C�ĺ�����С�ڵ�D�ĺ����꣩����P��ĺ�����Ϊm�����ú���m�Ĵ���ʽ��ʾ��C�ĺ����ꣻ
��3���ڣ�2���������£�����C���߶�AB�ϣ�����BOCΪ����������ʱ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��գ�
��1����ͼ1����Ϊ��1����2������֪��
��2����3���������������� ������ ���� ����
���ԡ�1����3��
����AB��CD�������� �������� ���� ������
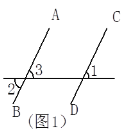
��2����ͼ2����Ϊ��1��110�㣨��֪��
��1����2��180�㣬���������������� ��������
���ԡ�2�������� ������
����Ϊ��3��70�㣬����֪��
���ԡ�2����3��
����a��b������������ ������������������������
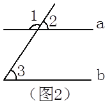
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��������ס���������Ʒ����֪�Ľ������ҵĽ��۵�һ�룬��3������Ʒ��1������Ʒǡ����200Ԫ���ס���������Ʒ���ۼ�ÿ���ֱ�Ϊ80Ԫ��130Ԫ�����̵�����ò�����6710Ԫ�Ҳ�����6810Ԫ������������Ʒ��100����
��1������������Ʒ�Ľ��ۣ�
��2�����̵��м��ֽ������������ֽ��������ɻ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з��̣���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() �������Ƕ�Ԫһ�η��̵��ǣ� ��
�������Ƕ�Ԫһ�η��̵��ǣ� ��
A.��B.�٢�C.�٢�D.�٢ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽�ѧ���Ŀ����Ķ�����������ȡ��50��ѧ������ͳ������ƽ��ÿ��Ŀ����Ķ�ʱ�䣯(��λ��min)��Ȼ�������������ݻ��Ƴ����²�������ͳ��ͼ����

����ͼ�����ṩ����Ϣ���ش��������⣺
(1)a��_____��b��_____��
(2)��Ƶ���ֲ�ֱ��ͼ����������
(3)����У��1 000��ѧ���������ж���ѧ��ƽ��ÿ��Ŀ����Ķ�ʱ�䲻����50min?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��˫����y= ![]() ������A��1��2��������A��y��Ĵ��ߣ�����ΪB����˫����y=��
������A��1��2��������A��y��Ĵ��ߣ�����ΪB����˫����y=�� ![]() �ڵ�C��ֱ��y=m��m��0���ֱ�˫����y=��
�ڵ�C��ֱ��y=m��m��0���ֱ�˫����y=�� ![]() ��y=
��y= ![]() �ڵ�P��Q��
�ڵ�P��Q��
��1����k��ֵ��
��2������OAPΪֱ�������Σ����P�����ꣻ
��3����OCQ�������ΪS��OCQ �� ��OAP�������ΪS��OAP���ԱȽ�S��OCQ��S��OAP�Ĵ�С��ֱ��д�����ۣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com