
【题目】如图,双曲线y= ![]() 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣ ![]() 于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣ ![]() 、y=
、y= ![]() 于点P、Q.
于点P、Q.
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ , △OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论).
【答案】
(1)解:∵双曲线y= ![]() 经过点A(1,2),
经过点A(1,2),
∴k=1×2=2;
(2)解:设P(﹣ ![]() ,m),
,m),
∵A(1,2),
∴OA2=12+22=5,AP2=(1+ ![]() )2+(2﹣m)2,OP2=(
)2+(2﹣m)2,OP2=( ![]() )2+m2,
)2+m2,
当∠AOP=90°时,
∵OA2+OP2=AP2,即5+( ![]() )2+m2=(1+
)2+m2=(1+ ![]() )2+(2﹣m)2,解得m=±3,
)2+(2﹣m)2,解得m=±3,
∴P1(﹣6,3),P2(6,﹣3);
当∠OAP=90°时,
∵OA2+AP2=OP2,即5+(1+ ![]() )2+(2﹣m)2=(
)2+(2﹣m)2=( ![]() )2+m2,解得m=
)2+m2,解得m= ![]() ,
,
∴P3( ![]() ),P4(
),P4( ![]() );
);
当∠APO=90°时,此种情况不存在;
(3)解:∵A(1,2),
∴C(﹣9,2).
设P(﹣ ![]() ,m),则Q(
,m),则Q( ![]() ,m),
,m),
分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,
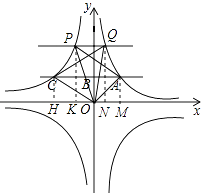
∵点A、Q在反比例函数y= ![]() 的图象上,
的图象上,
∴S△AOM=S△QON=1.
∵点C、P在反比例函数y=﹣ ![]() 的图象上,
的图象上,
∴S△COH=S△POK=9.
S△OCQ=S梯形CHNQ﹣S△COH﹣S△POK,S△OAP=S梯形AMKP﹣S△AOM﹣S△POK,
∴S△OCQ﹣S△OAP=S梯形CHNQ﹣S梯形AMKP,
∵梯形CHNQ与梯形AMKP的上底与下底相同,
∴只要比较HN与KM的大小即可,
∵HN﹣KM=(9+ ![]() )﹣(1+
)﹣(1+ ![]() )=8﹣
)=8﹣ ![]() ,
,
∴当m=±2时,HN=KM,即S△OCQ=S△OAP;
当m>2或m<﹣2时,8﹣ ![]() >0,即S△OCQ>S△OAP;
>0,即S△OCQ>S△OAP;
当﹣2<m<2时,8﹣ ![]() <0,即S△OCQ<S△OAP.
<0,即S△OCQ<S△OAP.
【解析】(1)将点A的坐标代入反比例函数解析式即可求出k的值。
(2)设出点P的坐标,根据点A、P、O的坐标,分别求出OA2、AP2、OP2,再分三种情况讨论:当∠AOP=90°时,得出OA2+OP2=AP2,建立关于m的方程,求解即可求出点P的坐标;当∠OAP=90°时,则OA2+AP2=OP2,建立关于m的方程,求解即可求出点P的坐标;当∠APO=90°时,此种情况不存在。
(3)根据点A(1,2)可得出C(﹣9,2).分别设出点P、Q的坐标,分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,再由反比例函数图像上的点的坐标特点得出△AOM、△QON、△COH、△POK的面积,然后根据S△OCQ﹣S△OAP=S梯形CHNQ﹣S梯形AMKP,由于梯形CHNQ与梯形AMKP的上底与下底相同,因此只需比较HN与KM的大小即可,从而分三种情况讨论,可求得结论。
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
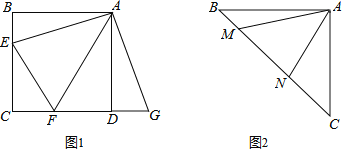
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双蓉服装店老板到厂家购A、B两种型号的服装,若购A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元.
(1)求A、B两种型号的服装每件分别为多少元?
(2)若销售一件A型服装可获利18元,销售一件B型服装可获利30元,根据市场需要,服装店老板决定:购进A型服装的数量要比购进B型服装的数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后可使总的获利不少于699元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识生成)
通常情况下、用两种不同的方法计算同一图形的面积,可以得到一个恒等式.
(1)如图 1,请你写出![]() 之间的等量关系是
之间的等量关系是
(知识应用)
(2)根据(1)中的结论,若![]() ,则
,则![]()
(知识迁移)
类似地,用两种不同的方法计算同一几何体的情况,也可以得到一个恒等式.如图 ![]() 是边长为
是边长为![]() 的正方体,被如图所示的分割成
的正方体,被如图所示的分割成 ![]() 块.
块.
(3)用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式可以是
(4)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D, BE⊥MN于E.
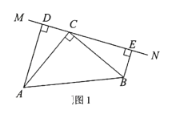
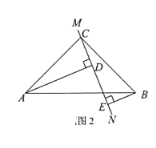
(1)当直线MN绕点C旋转到图1的位置时,求证:△ADC≌△CEB;
(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE的等量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com