Question

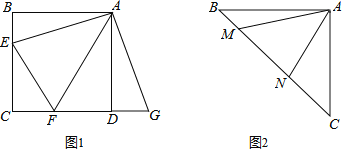
【题目】（1）如图，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．

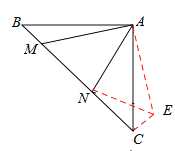
（2）如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题（1）证△ADG≌△ABE，△FAE≌△GAF，根据全等三角形的性质求出即可.

（2）过点C作CE⊥BC，垂足为点C，截取CE，使CE=BM．连接AE、EN．通过证明△ABM≌△ACE（SAS）推知全等三角形的对应边AM=AE、对应角∠BAM=∠CAE；然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°，所以△MAN≌△EAN（SAS），故全等三角形的对应边MN=EN；最后由勾股定理得到EN2=EC2+NC2即MN2=BM2+NC2．

试题解析：解：（1）证明：∵四边形ABCD是正方形，∴∠ABE=∠ADG，AD=AB.

在△ABE和△ADG中，∵，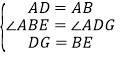

∴△ABE≌△ADG（SAS）.∴∠BAE=∠DAG，AE="AG." ∴∠EAG=90°.

在△FAE和△GAF中，∵，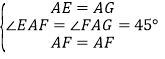

∴△FAE≌△GAF（SAS），∴EF=FG.

（2）如答图，过点C作CE⊥BC，垂足为点C，截取CE，使CE=BM，连接AE、EN．

∵AB=AC，∠BAC=90°，∴∠B=∠C=45°．

∵CE⊥BC，∴∠ACE=∠B=45°．

在△ABM和△ACE中，∵，

∴△ABM≌△ACE（SAS）．∴AM=AE，∠BAM=∠CAE．

∵∠BAC=90°，∠MAN=45°，∴∠BAM+∠CAN=45°．

∴由∠BAM=∠CAE，得∠MAN=∠EAN=45°．

在△MAN和△EAN中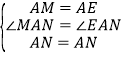，∵，∴△MAN≌△EAN（SAS）．∴MN=EN．

在Rt△ENC中，由勾股定理，得EN2=EC2+NC2．∴MN2=BM2+NC2．

∵BM=1，CN=3，∴MN2=12+32. ∴MN=.