
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)若CE=12,CF=5,求OC的长;
(2)当点O运动到何处时,四边形AECF是矩形,并说明理由;

【答案】(1)6.5;(2)点O运动到AC的中点,理由见解析.
【解析】
(1)根据角平分线和平行线性质得到∠FCE=90°,OE=OC=OF,根据直角三角形斜边上的中线等于斜边的一半得到OC=![]() EF,根据勾股定理求出EF,即可求出AC;
EF,根据勾股定理求出EF,即可求出AC;
(2)由(1)得出的EO=CO=FO,点O运动到AC的中点时,则有EO=CO=FO=AO,所以这时四边形AECF是矩形.
解:(1)∵MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,
∴∠OCE=∠ECB,∠OCF=∠FCD,
∵MN∥BC,
∴∠OEC=∠ECB,∠OFC=∠FCD,
∴∠OEC=∠OCE,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴OE=OF,
∵∠OEC=∠OCE,∠OFC=∠OCF,
∴∠OEC+∠OFC=∠OCE+∠OCF=90°.
∵CE=12,CF=5,
∴EF=![]() =13,
=13,
∴OC=![]() EF=6.5;
EF=6.5;
(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
理由:当O为AC的中点时,AO=CO.
∵EO=FO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴平行四边形AECF是矩形.
故答案为:(1)6.5;(2)点O运动到AC的中点,理由见解析.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,有下列说法:
①食堂离小明家0.4km;
②小明从食堂到图书馆用了3min;
③图书馆在小明家和食堂之间;
④小明从图书馆回家的平均速度是0.04km/min.
其中正确的有( )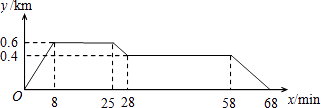
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
(1)点D的坐标为 , 点C的坐标为;
(2)若点P是对角线OC上一动点,点E(0,﹣ ![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.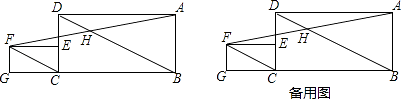
(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
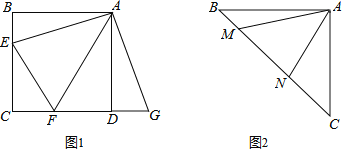
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个项点的坐标分别为A (3. 3),B (-3, 0), C (0. -2).
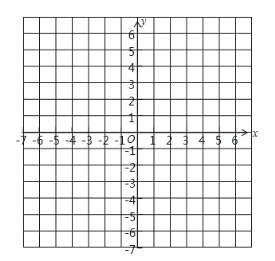
(1)在下面的平面直角坐标系中分别描出A,B, C三点,并画出△ABC;
(2)将(1)中的△ABC向上平移3个单位长度,向左中移2个单位长度,得到△![]() 在图中画出△
在图中画出△![]() ,请分别写出A1、B1、C1三点的坐标.
,请分别写出A1、B1、C1三点的坐标.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在右边的平面直角坐标系中描出以下三点:![]() 、
、![]() 、
、![]() 并回答如下问题:
并回答如下问题:
![]() 在平面直角坐标系中画出△ABC;
在平面直角坐标系中画出△ABC;
![]() 在平面直角坐标系中画出△A′B′C′;使它与
在平面直角坐标系中画出△A′B′C′;使它与![]() 关于x轴对称,并写出点C′的坐标______;
关于x轴对称,并写出点C′的坐标______;
![]() 判断△ABC的形状,并说明理由.
判断△ABC的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com