
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

【答案】(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,证明见解析;
(2)点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
【解析】(1)①根据图形猜想得出所求角度数即可;
②根据图形猜想得出所求角度数即可;
③猜想得到三角关系,理由为:延长AE与DC交于F点,由AB与DC平行,利用两直线平行内错角相等得到一对角相等,再利用外角性质及等量代换即可得证;
(2)分四个区域分别找出三个角关系即可.
解:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
“点睛”此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.


科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测。一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M、N为该岛的东西两端点)最近距离为14km(即MC=14km)。在A点测得岛屿的西端点M在点A的东北方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东60°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点M、N之间的距离(结果保留根号)。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,若AB∥DE,∠B=135°,∠D=145°,你能求出∠C的度数吗?
(2)在AB∥DE的条件下,你能得出∠B、∠C、∠D之间的数量关系吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,给出下列论断:
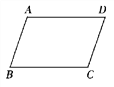
①AB∥DC;②AD∥BC;③AB=AD;④∠A=∠C;⑤AD=BC.
以上面论断中的两个作为题设,再从余下的论断中选一个作为结论,并用“如果……,那么……”的形式写出一个真命题.
答:_____________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中与多项式2x﹣(﹣3y﹣4z)相等的是( )
A.2x+(﹣3y+4z)
B.2x+(3y﹣4z)
C.2x+(﹣3y﹣4z)
D.2x+(3y+4z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com