
【题目】(1)如图,若AB∥DE,∠B=135°,∠D=145°,你能求出∠C的度数吗?
(2)在AB∥DE的条件下,你能得出∠B、∠C、∠D之间的数量关系吗?并说明理由.

【答案】(1)80°;(2)∠B+∠C+∠D=360°.
【解析】试题分析:(1)作CF∥AB,则CF∥DE,根据两直线平行,同旁内角互补可以分别求出∠BCF和∠DCF的度数,即可求出∠BCD的度数;(2)∠B+∠BCD+∠D=360°,由两直线平行,同旁内角互补可得:∠B+∠BCF=180°,∠D+∠DCF=180°,所以∠B+∠BCF+∠D+∠DCF=180°,即∠B+∠BCD+∠D=360°.
试题解析:
如图,作CF∥AB,则CF∥DE,
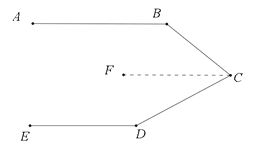
∴∠B+∠BCF=180°,∠D+∠DCF=180°,
∵∠B=135°,∠D=145°,
∴∠BCF=45°,∠DCF=35°,
∴∠BCD=80°;
(2)∠B+∠BCD+∠D=360°,
如上图,∵CF∥AB,则CF∥DE,
∴∠B+∠BCF=180°,∠D+∠DCF=180°,
∴∠B+∠BCF+∠D+∠DCF=360°,
即∠B+∠BCD+∠D=360°.


科目:初中数学 来源: 题型:
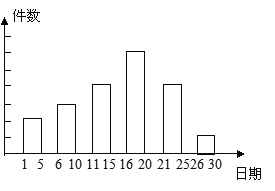
【题目】在我校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12件. 请你回答:
(1)本次活动共有________件作品参赛;各组作品件数的中位数是________件.
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州文化用品市场A商家独家销售某种儿童玩具,每件进价为40元.经过市场调查,一周的销售量![]() 件与销售单价
件与销售单价![]() (
(![]() ≥45)元/件的关系如下表:
≥45)元/件的关系如下表:
销售单价 | … | 45 | 55 | 70 | 75 | … |
一周的销售量 | … | 550 | 450 | 300 | 250 | … |
(1)直接写出![]() 与
与![]() 的函数关系式: ;
的函数关系式: ;
(2)设一周的销售利润为W元,请求出W与![]() 的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润(W)随着销售单价(
的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润(W)随着销售单价(![]() )的增大而增大?
)的增大而增大?
(3)A商家决定将该玩具一周的销售利润全部捐给孤儿院,在商家购进该商品的钱款数额不超过8000元的情况下,请你求出该商家最大捐款数额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现2个正面向上一个反面向上,则小亮赢;若出现一个正面向上2个反面向上,则小文赢.
(1)请利用树状图或列表法或枚举法描述三人获胜的概率;
(2)分别求出小强、小亮、小文三位同学获胜的概率,并回答谁赢的概率最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com