
【题目】温州文化用品市场A商家独家销售某种儿童玩具,每件进价为40元.经过市场调查,一周的销售量![]() 件与销售单价
件与销售单价![]() (
(![]() ≥45)元/件的关系如下表:
≥45)元/件的关系如下表:
销售单价 | … | 45 | 55 | 70 | 75 | … |
一周的销售量 | … | 550 | 450 | 300 | 250 | … |
(1)直接写出![]() 与
与![]() 的函数关系式: ;
的函数关系式: ;
(2)设一周的销售利润为W元,请求出W与![]() 的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润(W)随着销售单价(
的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润(W)随着销售单价(![]() )的增大而增大?
)的增大而增大?
(3)A商家决定将该玩具一周的销售利润全部捐给孤儿院,在商家购进该商品的钱款数额不超过8000元的情况下,请你求出该商家最大捐款数额是多少元?
【答案】(1)![]() (2)当
(2)当![]() 时一周的销售利润(W)随着销售单价(
时一周的销售利润(W)随着销售单价(![]() )的增大而增大(3)该商家最大捐款数额是8000元
)的增大而增大(3)该商家最大捐款数额是8000元
【解析】(1)设y=kx+b,把点的坐标代入解析式,求出k、b的值,即可得出函数解析式;
(2)根据利润=(售价-进价)×销售量,列出函数关系式,继而确定销售利润随着销售单价的增大而增大的销售单价的范围;
(3)根据购进该商品的贷款不超过8000元,求出进货量,然后求最大销售额即可.
解:(1)![]() 与
与![]() 的函数关系式:
的函数关系式: ![]()
(2)由题可得: ![]()
∴ W与![]() 的函数关系式为:
的函数关系式为: ![]()
又由题知: ![]()
![]()
∵![]()
![]() 当
当![]() 时一周的销售利润(W)随着销售单价(
时一周的销售利润(W)随着销售单价(![]() )的增大而增大
)的增大而增大
(3)由题得: ![]()
![]()
结合(2)知: ![]()
![]() 当
当![]() 时,W随着x的增大而减小
时,W随着x的增大而减小
∴ 在![]() 内,当
内,当![]() 时,W最大,W=8000
时,W最大,W=8000
∴该商家最大捐款数额是8000元


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,若AB∥DE,∠B=135°,∠D=145°,你能求出∠C的度数吗?
(2)在AB∥DE的条件下,你能得出∠B、∠C、∠D之间的数量关系吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,给出下列论断:
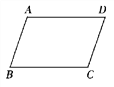
①AB∥DC;②AD∥BC;③AB=AD;④∠A=∠C;⑤AD=BC.
以上面论断中的两个作为题设,再从余下的论断中选一个作为结论,并用“如果……,那么……”的形式写出一个真命题.
答:_____________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.

(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中与多项式2x﹣(﹣3y﹣4z)相等的是( )
A.2x+(﹣3y+4z)
B.2x+(3y﹣4z)
C.2x+(﹣3y﹣4z)
D.2x+(3y+4z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,Rt△ABC中,∠ACB=90°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(2)如图2,在△ABC中,∠ACB=40°,点D、E在直线AB上,且AD=AC,BE=BC,则∠DCE的度数;
(3)在△ABC中,∠ACB=n°(0<n<180°),点D、E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
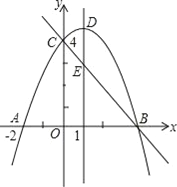
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题:
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com