
【题目】请在右边的平面直角坐标系中描出以下三点:![]() 、
、![]() 、
、![]() 并回答如下问题:
并回答如下问题:
![]() 在平面直角坐标系中画出△ABC;
在平面直角坐标系中画出△ABC;
![]() 在平面直角坐标系中画出△A′B′C′;使它与
在平面直角坐标系中画出△A′B′C′;使它与![]() 关于x轴对称,并写出点C′的坐标______;
关于x轴对称,并写出点C′的坐标______;
![]() 判断△ABC的形状,并说明理由.
判断△ABC的形状,并说明理由.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)若CE=12,CF=5,求OC的长;
(2)当点O运动到何处时,四边形AECF是矩形,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.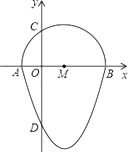
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E、F分别是AC、BC的中点,直线EF与⊙O交于点G、H.若⊙O的半径为2,则GE+FH的最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形,那么我们称这个三角形为“活三角形”,这条直线称为该“活三角形”的“生命线”.
(1)小明在研究“活三角形”问题时(如图),他发现,在△ABC中,若∠BAC = 3∠C时,这个△ABC一定是“活三角形”.点D在BC边上一点,联结AD,他猜测:当∠DAC = ∠C时,AD就是这个三角形的“生命线”,请你帮他说明AD是△ABC的“生命线”的理由.

(2)如小明研究结果可以总结为:有一个内角是另一个内角的3倍时,该三角形是一个“活三角形”.
请通过自己操作研究,并根据上诉结论,总结“活三角形”的其他特征.
(注意从三角形边、角特征及相互间关系总结)
,该三角形是一个“活三角形”.
,该三角形是一个“活三角形”.
(3)如果一个等腰三角形是一个“活三角形”那么它的顶角大小为: 度.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.根据以上信息解决下列问题:
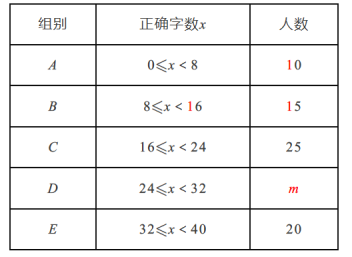

(1)在统计表中,m= ,n= ,并补全直方图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 度;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6![]() B. 6C. 3
B. 6C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法①△ABC中,若∠A+∠B=90°,则△ABC是直角三角形;②已知正n边形的一个内角为140,则这个正多边形的边数是9;③一个多边形的内角中最多有3个锐角;④三角形的外角一定大于内角;⑤若不等式组![]() 的整数解恰好有2个,则m的取值范围是
的整数解恰好有2个,则m的取值范围是![]() ,其中说法正确的是_____________________(填写说法正确的序号)
,其中说法正确的是_____________________(填写说法正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com