【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是（ ）
A. 6
B. 6C. 3D. 3+3
【答案】A
【解析】
试题由边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，利用勾股定理的知识求出BC′的长，再根据等腰直角三角形的性质，勾股定理可求BO，OD′，从而可求四边形ABOD′的周长．
连接BC′， ∵旋转角∠BAB′=45°，∠BAD′=45°， ∴B在对角线AC′上， ∵B′C′=AB′=3，
在Rt△AB′C′中，AC′=
=3
， ∴B′C=3﹣3，
在等腰Rt△OBC′中，OB=BC′=3﹣3， 在直角三角形OBC′中，OC=（3﹣3）=6﹣3，
∴OD′=3﹣OC′=3﹣3，
∴四边形ABOD′的周长是：2AD′+OB+OD′=6+3﹣3+3﹣3=6
科目：初中数学 来源： 题型：
【题目】某路公交车从起点经过A、B、C、D站到达终点，一路上下乘客如下表所示。（用正数表示上车的人数，负数表示下车的人数）
（1）到终点下车还有________人.
（2）车行驶在那两站之间车上的乘客最多？________站和________站
（3）若每人乘坐一站需买票1元，问该车出车一次能收入多少钱？写出算式。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，已知正方形ABCD的边长为1，点P是AD边上的一个动点，点A关于直线BP的对称点是点Q，连接PQ、DQ、CQ、BQ，设AP＝x．
（1）BQ＋DQ的最小值是_______，此时x的值是_______；
（2）如图②，若PQ的延长线交CD边于点E，并且∠CQD＝90°．
①求证：点E是CD的中点； ②求x的值．
（3）若点P是射线AD上的一个动点，请直接写出当△CDQ为等腰三角形时x的值．
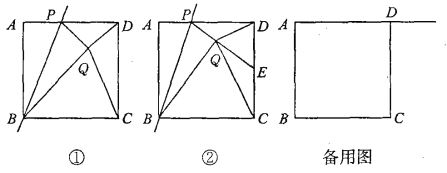
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的
少20人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：
（1）报两门课的共有多少人？
（2）调动后，报名第一门课的人数为 人，第二门课人数为 人．
（3）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,直线y1=
x+1与x轴交于点A,与y轴交于点B，与反比例函数y2=
（x＞0）的图象交于点C，且AB=BC．
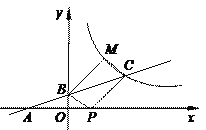
(1) 求点C的坐标和反比例函数y2的解析式；
(2) 点P在x轴上，反比例函数y2图象上存在点M，使得四边形BPCM为平行四边形，求
BPCM的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”
设井深为x尺，根据题意列方程，正确的是（ ）
A. 3（x+4）=4（x+1） B. 3x+4=4x+1
C. 3（x﹣4）=4（x﹣1） D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请根据图中提供的信息,回答下列问题
（1）一个暖瓶与一个水杯分别是多少元?
（2）甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定： 这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是菱形，对角线AC与BD相交于O，AB＝6cm， ∠BAO＝30°，点F为AB的中点.
（1）求OF的长度；
（2）求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com