
【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形,那么我们称这个三角形为“活三角形”,这条直线称为该“活三角形”的“生命线”.
(1)小明在研究“活三角形”问题时(如图),他发现,在△ABC中,若∠BAC = 3∠C时,这个△ABC一定是“活三角形”.点D在BC边上一点,联结AD,他猜测:当∠DAC = ∠C时,AD就是这个三角形的“生命线”,请你帮他说明AD是△ABC的“生命线”的理由.

(2)如小明研究结果可以总结为:有一个内角是另一个内角的3倍时,该三角形是一个“活三角形”.
请通过自己操作研究,并根据上诉结论,总结“活三角形”的其他特征.
(注意从三角形边、角特征及相互间关系总结)
,该三角形是一个“活三角形”.
,该三角形是一个“活三角形”.
(3)如果一个等腰三角形是一个“活三角形”那么它的顶角大小为: 度.(直接写出结果即可)
【答案】(1)详见解析;(2)有一个内角是另一个内角2倍时;有一个内角为直角时;(3)90°,108°,36°,![]()
【解析】
(1)证明△ADC和△ABD为等腰三角形即可;
(2)作∠CAD=∠C,则∠ADB=2∠C,当∠ABD=2∠C时,∠ABD=∠ADB,则△ABC为“活三角形”;由直角三角形斜边的中线等于斜边的一半,易证直角三角形为“活三角形”;
(3)分四种情况讨论,根据三角形内角和为180°建立方程,解方程求出顶角即可.
解:(1)∵∠DAC =∠C,
∴∠ADB=2∠C,△ADC为等腰三角形,
又∵∠BAC=3∠C,
∴∠BAD=2∠C=∠ADB,
∴△ABD为等腰三角形,
∴AD是△ABC的“生命线”;
(2)∠ADB=2∠C,当∠ABD=2∠C时,∠ABD=∠ADB,则△ABC为“活三角形”,
即:有一个内角是另一个内角的2倍时,该三角形是一个“活三角形”;
当∠BAC=90°,AD为斜边BC的中线,则△ABC为“活三角形”,
即:有一个内角为直角时,该三角形是一个“活三角形”,
故答案为:有一个内角是另一个内角的2倍时;有一个内角为直角时
(3)①由(2)可知,直角三角形为“活三角形”,故等腰直角三角形也为“活三角形”,即顶角为90°;
②如图,△ABC为等腰三角形,AB=AC,
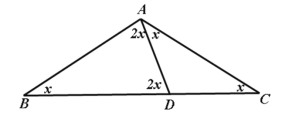
则有![]() ,
,
解得:![]() ,
,
顶角∠BAC=108°;
③如图,△ABC为等腰三角形,AB=AC,
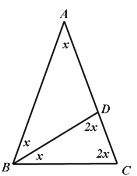
则有,![]() 。,
。,
解得:![]() ,
,
顶角∠BAC=36°;
④如图,△ABC为等腰三角形,AB=AC,
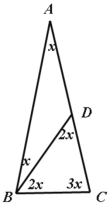
则![]() ,
,
解得:![]() ,
,
即顶角∠BAC=![]() ,
,
综上:顶角为90°,108°,36°,![]() .
.


科目:初中数学 来源: 题型:
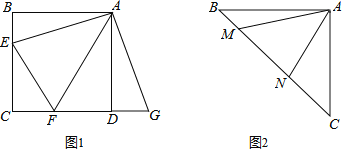
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D, BE⊥MN于E.
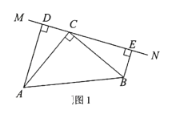
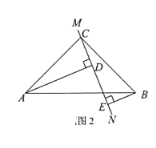
(1)当直线MN绕点C旋转到图1的位置时,求证:△ADC≌△CEB;
(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE的等量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
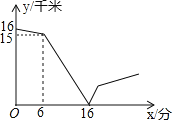
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示
(1)甲的速度为______千米/分,乙的速度为______千米/分
(2)当乙到达终点A后,甲还需______分钟到达终点B
(3)请通过计算回答:当甲、乙之间的距离为10千米时,甲出发了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动,设动点运动时间为t秒.
(1)求AD的长;
(2)当P、C两点的距离为![]() 时,求t的值;
时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t值,使得![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.

备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在右边的平面直角坐标系中描出以下三点:![]() 、
、![]() 、
、![]() 并回答如下问题:
并回答如下问题:
![]() 在平面直角坐标系中画出△ABC;
在平面直角坐标系中画出△ABC;
![]() 在平面直角坐标系中画出△A′B′C′;使它与
在平面直角坐标系中画出△A′B′C′;使它与![]() 关于x轴对称,并写出点C′的坐标______;
关于x轴对称,并写出点C′的坐标______;
![]() 判断△ABC的形状,并说明理由.
判断△ABC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是96分,请问小红在竞赛中答对了多少题?
(2)小明也参加了竞赛,考完后他说:“这次竟赛中我一定能拿到110分.”请问小明有没有可能拿到110分?试用方程的知识来说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com