
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D, BE⊥MN于E.
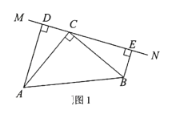
(1)当直线MN绕点C旋转到图1的位置时,求证:△ADC≌△CEB;
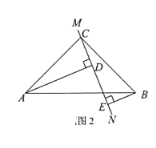
(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE的等量关系?并说明理由.
【答案】(1)见解析;(2)DE=AD-BE,理由见解析
【解析】
(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,即可得到答案.
解:(1)证明:如图1,
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
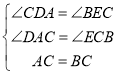 ,
,
∴△ADC≌△CEB(AAS);
(2)结论:DE=AD-BE.
理由:如图2,∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
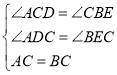 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.


科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间/(单位:min),然后利用所得数据绘制成如下不完整的统计图表.

根据图表中提供的信息,回答下列问题:
(1)a=_____,b=_____;
(2)将频数分布直方图补充完整;
(3)若该校共1 000名学生,估计有多少学生平均每天的课外阅读时间不少于50min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线y= ![]() 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣ ![]() 于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣ ![]() 、y=
、y= ![]() 于点P、Q.
于点P、Q.
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ , △OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.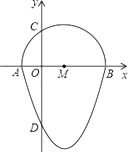
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=∠D.点EF分别在AB、CD上.连接AC,分别交DE、BF于G、H.求证:∠1+∠2=180°
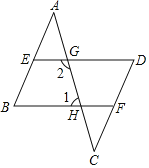
证明:∵AB∥CD,
∴∠B=_____._____
又∵∠B=∠D,
∴_____=_____.(等量代换)
∴_____∥_____._____
∴∠l+∠2=180°._____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形,那么我们称这个三角形为“活三角形”,这条直线称为该“活三角形”的“生命线”.
(1)小明在研究“活三角形”问题时(如图),他发现,在△ABC中,若∠BAC = 3∠C时,这个△ABC一定是“活三角形”.点D在BC边上一点,联结AD,他猜测:当∠DAC = ∠C时,AD就是这个三角形的“生命线”,请你帮他说明AD是△ABC的“生命线”的理由.

(2)如小明研究结果可以总结为:有一个内角是另一个内角的3倍时,该三角形是一个“活三角形”.
请通过自己操作研究,并根据上诉结论,总结“活三角形”的其他特征.
(注意从三角形边、角特征及相互间关系总结)
,该三角形是一个“活三角形”.
,该三角形是一个“活三角形”.
(3)如果一个等腰三角形是一个“活三角形”那么它的顶角大小为: 度.(直接写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com