[题目]如图.利用标杆BE测量建筑物的高度.如果标杆BE长1.2m.测得AB=1.6m.BC=8.4m.楼高CD是多少? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，利用标杆BE测量建筑物的高度，如果标杆BE长1.2m，测得AB=1.6m，BC=8.4m，楼高CD是多少？

【答案】解：解：∵EB⊥AC，DC⊥AC，

∴EB∥DC，

∴△ABE∽△ACD，

∴ ，

∵BE=1.2，AB=1.6，BC=8.4，

∴AC=10，

∴ ，

∴CD=7.5．

答：楼高CD是7.5m．

【解析】先根据题意得出△ABE∽△ACD，再根据相似三角形的对应边成比例即可求出CD的值．
【考点精析】根据题目的已知条件，利用相似三角形的应用的相关知识可以得到问题的答案，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形，那么我们称这个三角形为“活三角形”，这条直线称为该“活三角形”的“生命线”．

（1）小明在研究“活三角形”问题时（如图），他发现，在△ABC中，若∠BAC = 3∠C时，这个△ABC一定是“活三角形”．点D在BC边上一点，联结AD，他猜测：当∠DAC = ∠C时，AD就是这个三角形的“生命线”，请你帮他说明AD是△ABC的“生命线”的理由．

（2）如小明研究结果可以总结为：有一个内角是另一个内角的3倍时，该三角形是一个“活三角形”．

请通过自己操作研究，并根据上诉结论，总结“活三角形”的其他特征．

（注意从三角形边、角特征及相互间关系总结）

，该三角形是一个“活三角形”．

（3）如果一个等腰三角形是一个“活三角形”那么它的顶角大小为：度．（直接写出结果即可）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在ABCD中，E、F为边BC上两点，且BE＝CF，AF＝DE．

（1）求证：△ABF≌△DCE；

（2）四边形ABCD是矩形吗？为什么？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】小东家与学校之间是一条笔直的公路，早饭后，小东步行前往学校，途中发现忘带画板，停下给妈妈打电话，妈妈接到电话后，带上画板马上赶往学校，同时小东沿原路返回，两人相遇后，小东立即赶往学校，妈妈沿原路返回，16min时到家，假设小东始终以100m/min的速度步行，两人离家的距离y(单位：m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示：

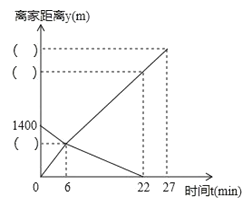
（1）小东打电话时，他离家_________m；

（2）填上图中空格相应的数据_________，_________，_________；

（3）小东和妈妈相遇后，妈妈回家的速度为_________m/min；

（4）_________min时，两人相距700m．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，长方体的长为15宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）

A. 20 B. 25 C. 30 D. 32

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列说法①△ABC中，若∠A+∠B=90°，则△ABC是直角三角形；②已知正n边形的一个内角为140，则这个正多边形的边数是9；③一个多边形的内角中最多有3个锐角；④三角形的外角一定大于内角；⑤若不等式组的整数解恰好有2个，则m的取值范围是，其中说法正确的是_____________________（填写说法正确的序号）