
【题目】如图,在平面直角坐标系中,直线 ![]() 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值.
【答案】
(1)解:(1)当x=0时,y=4;当y=0时,- ![]() x+4=0,x=3.
x+4=0,x=3.
∴A(3,0),B(0,4).
(2)解:设点C的横坐标为n.由(1)知AB= ![]() =5,
=5,
∴sin∠OBA= ![]() .
.
过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,
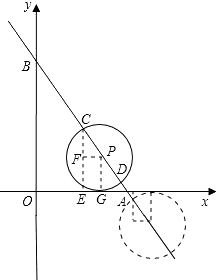
则∠FCP=∠OBA,PF=m-n.
①当m<3时,∵PC=PG=- ![]() m+4,
m+4,
∴PF=PCsin∠FCP=PCsin∠OBA,
∴m-n=(- ![]() m+4)×
m+4)× ![]() .
.
解得n= ![]() m-
m- ![]()
②当m>3时,PC=PG= ![]() m-4,PF=PCsin∠FCP=PCsin∠OBA,
m-4,PF=PCsin∠FCP=PCsin∠OBA,
∴m-n=( ![]() m-4)×
m-4)× ![]() .
.
解得n= ![]() m+
m+ ![]()
(3)解:当点C在线段AB上时,由(2)知,C点的横坐标n= ![]() m-
m- ![]() ,
,
以下两种情况△BOC为等腰三角形.
①当CB=CO时,
∵△OBA是直角三角形,∠BOA=90度.
∴此时C为AB的中点,
∴C点的横坐标为 ![]() .
.
∴ ![]() m-
m- ![]() =
= ![]() ,解得m=
,解得m= ![]() .
.
②当CB=OB时,
∵AB=5,
∴AC=AB-CB=1,
∴AE=ACcos∠OAB= ![]() .
.
∵OE+AE=OA,
∴ ![]() m-
m- ![]() +
+ ![]() =3,解得m=
=3,解得m= ![]() .
.
③当OC=OB时,因为OB>OA,所以C在线段BA的延长线上,即在线段AB上不存在点C,使OC=OB。
所以,当m= ![]() 或m=
或m= ![]() 时,△BOC为等腰三角形.
时,△BOC为等腰三角形.
【解析】(1)根据题意分别求出当x=0时和当y=0时,对应的函数值和自变量的值,即可求得点A、B的坐标。
(2)设点C的横坐标为n.利用勾股定理求出AB的长,过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,证得∠FCP=∠OBA,PF=m-n.分两种情况:①当m<3时;②当m>3时,得出PC=PG,再分别根据PF=PCsin∠FCP=PCsin∠OBA;PF=PCsin∠FCP=PCsin∠OBA,得出关于m、n的关系式,即可求出n的值。
(3)分三种情况:①当CB=CO时,根据点C的横坐标建立方程,求出m的值;②当CB=OB时,根据OE+AE=OA,建立关于m的方程,求解即可。
③在线段AB上不存在点C,使OC=OB。
【考点精析】掌握等腰三角形的性质和切线的性质定理是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:

(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() ,
,![]() 满足
满足![]() .
.
(1)求点![]() 与点
与点![]() 在数轴上对应的数
在数轴上对应的数![]() 和
和![]() ;
;
(2)现动点![]() 从点
从点![]() 出发,沿数轴向右以每秒
出发,沿数轴向右以每秒![]() 个单位长度的速度运动;同时,动点
个单位长度的速度运动;同时,动点![]() 从点
从点![]() 出发,沿数轴向左以每秒
出发,沿数轴向左以每秒![]() 个单位长度的速度运动,设点
个单位长度的速度运动,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
① 若点![]() 和点
和点![]() 相遇于点
相遇于点![]() , 求点
, 求点![]() 在数轴上表示的数;
在数轴上表示的数;
② 当点![]() 和点
和点![]() 相距
相距![]() 个单位长度时,直接写出
个单位长度时,直接写出![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 ![]() (元)与销售单价
(元)与销售单价 ![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,有下列说法:
①食堂离小明家0.4km;
②小明从食堂到图书馆用了3min;
③图书馆在小明家和食堂之间;
④小明从图书馆回家的平均速度是0.04km/min.
其中正确的有( )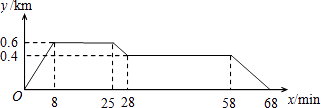
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级同学要在清明节到烈士陵园扫墓,计划制作![]() 朵小白花学生会主席小琳先做了
朵小白花学生会主席小琳先做了![]() 天,后来好朋友小雯也加入一起做了
天,后来好朋友小雯也加入一起做了![]() 天,最后比计划多制作
天,最后比计划多制作![]() 朵小白花.已知小雯每天比小琳少制作
朵小白花.已知小雯每天比小琳少制作![]() 朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花?
朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
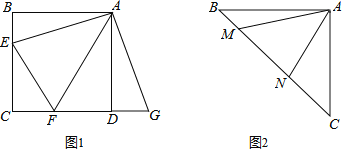
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com