
【题目】(1)(问题发现)如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一条直线上.填空:①线段BD,CE之间的数量关系为 ;②∠BEC = °.
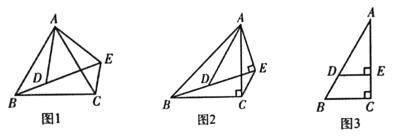
(2)(类比探究)如图2,△ABC和△ADE均为等腰直角三角形,∠ACB=∠AED=90°,AC=BC,AE=DE,点B,D,E在同一条直线上,请判断线段BD,CE之间的数量关系及∠BEC的度数,并给出证明.
(3)如图3,在△ABC中,∠ACB=90°,∠A=30°,AB = 5,点D在AB 边上,DE⊥AC于点E,AE = 3,将△ADE绕点A旋转,当DE所在直线经过点B时,CE的长是多少?(直接写出答案)
【答案】(1)①BD=CE,②60;(2)BD=![]() ,∠BEC=45
,∠BEC=45![]() .理由见解析;(3)
.理由见解析;(3)![]() 或
或![]()
【解析】
(1)利用等边三角形的性质和SAS可证明![]() ,则有
,则有![]() ,然后再利用
,然后再利用![]() 即可求出
即可求出![]() 的度数;
的度数;
(2)首先利用等腰直角三角形的性质和锐角三角函数得出![]() ,则有
,则有![]() ,
,![]() ,进而可求出
,进而可求出![]() ,再根据
,再根据![]() 即可得到
即可得到![]() ;
;
(3)分两种情况进行讨论:将△ADE绕点A顺时针旋转,DE所在直线经过点B时和将△ADE绕点A逆时针旋转,DE所在直线经过点B时,利用相似三角形的判定及性质求解即可.
解:(1)∵![]() 和
和![]() 均为等边三角形,
均为等边三角形,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,![]() .
.
理由如下:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]()
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
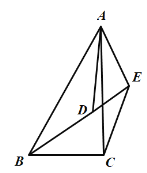
(3)如图,将△ADE绕点A逆时针旋转,DE所在直线经过点B时,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
如图,将△ADE绕点A顺时针旋转,DE所在直线经过点B时,

同理可得![]() ,
,
综上所述,CE的长度为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出随机摸球所有可能的结果;
(2)分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
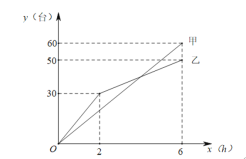
【题目】甲、乙两个电子团队维护一批电脑,维护电脑的台数y(台)与维护需要的工作时间x(h)(0≤x≤6)之间关系如图所示,请依据图象提供的信息解答下列问题:
(1)求乙队维护电脑的台数y(台)关于维护的时间x(h)的关系式;
(2)当x为多少时,甲、乙两队维护的电脑台数一样.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道组织志愿者活动,选派志愿者到小区服务.若每一个小区安排4人,那么还剩下78人;若每个小区安排8人,那么最后一个小区不足8人,但不少于4人.求这个街道共选派了多少名志愿者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在一个不透明的盒子中装有4小球,4个小球上分别标有数字1,﹣2,3,4,这些小球除标注的数字外其他都相同,将小球搅匀.
(1)从盒子中任意摸出一个小球,恰好摸出标有奇数小球的概率是: ;
(2)先从盒子中任意摸出一个小球,再从余下的3个小球中任意摸出一个小球,请用树状图或列表法求摸出的两个小球标有数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行汉字听写大赛,学习对参赛者获奖情况进行统计,根据比赛成绩列出统计表,并绘制了扇形统计图
(1)参加此次比赛的学生共______________人.
(2)![]()
(3)若从一等奖中随机抽取两名学生,参加市级汉字听写大赛,请用树状图或列表的方法,求出所选的两名学生正好为一男一女的概率.
等次 | 男生 | 女生 |
一等奖 | 3 | m |
二等奖 | 6 | 12 |
三等奖 | 8 | 9 |
鼓励奖 | 6 | n |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+1)(x﹣m)(a为非零常数,1<m<2),当x<﹣1时,y随x的增大而增大,说法正确的是( )
A.若图象经过点(0,1),则﹣![]() <a<0
<a<0
B.若x>﹣![]() 时,则y随x的增大而增大
时,则y随x的增大而增大
C.若(﹣2020,y1),(2020,y2)是函数图象上的两点,则y1<y2
D.若图象上两点(![]() ,y1),(
,y1),(![]() +n,y2)对一切正数n,总有y1>y2,则
+n,y2)对一切正数n,总有y1>y2,则![]() ≤m<2
≤m<2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com