练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下：在一个不透明的袋子中装有编号1-4的四个球（除编号外都相同）,从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜．

    （1）请用列表或画树状图的方法表示出随机摸球所有可能的结果；

    （2）分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗？

    【答案】（1）见解析 （2），；公平

    【解析】

    (1)根据题意，列出树状图，即可得到答案；

    (2)根据概率公式，分别求出小亮和小丽获胜的概率,即可.

    （1）画树状图如下：

    两数和的所有可能结果为：2,3,4,5,3,4,5,6,4,5,6,7,5,6,7,8共16种．

    （2）∵两次数字之和大于5的结果数为6,

    ∴小亮获胜的概率,

    ∵两次数字之和小于5的结果数为6,

    ∴小丽获胜的概率,

    ∴此游戏是公平的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

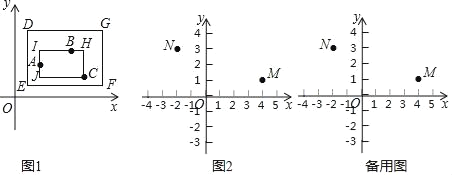
    【题目】平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”．在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“最佳三点矩形”．

    如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“最佳三点矩形”．

    如图2，已知M（4，1），N（﹣2，3），点P（m，n）．

    （1）①若m＝1，n＝4，则点M，N，P的“最佳三点矩形”的周长为　 　，面积为　 　；

    ②若m＝1，点M，N，P的“最佳三点矩形”的面积为24，求n的值；

    （2）若点P在直线y＝﹣2x+4上．

    ①求点M，N，P的“最佳三点矩形”面积的最小值及此时m的取值范围；

    ②当点M，N，P的“最佳三点矩形”为正方形时，求点P的坐标；

    （3）若点P（m，n）在抛物线y＝ax2+bx+c上，且当点M，N，P的“最佳三点矩形”面积为12时，﹣2≤m≤﹣1或1≤m≤3，直接写出抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠A=30°，直线a∥b，顶点C在直线b上，直线a交AB于点D，交AC于点E，若∠1=145°，则∠2的度数是( )

    A.30°B.35°C.40°D.45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

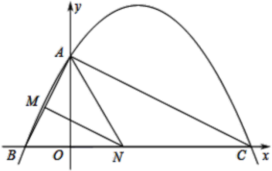
    【题目】如图，已知二次函数y＝ax2＋bx＋4的图象与x轴交于点B(－2，0)、点C(8，0)两点，与y轴交于点A．

    (1)求二次函数的表达式；

    (2)连接AC、AB，若点N在线段BC上运动(不与点B、C重合)，过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求N点的坐标；

    (3)连接OM，在(2)的结论下，线段AC上有一动点P，连接PM，求PM＋PC的值最小时，点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是等边三角形，点D为平面内一点，连接DB、DC，∠BDC＝120°．

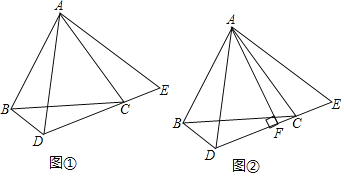
    （1）如图①，当点D在BC下方时，连接AD，延长DC到点E，使CE＝BD，连接AE．

    ①求证：△ABD≌△ACE；

    ②如图②，过点A作AF⊥DE于点F，直接写出线段AF、BD、DC间的数量关系；

    （2）若AB＝2，DC＝6，直接写出点A到直线BD的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图像与坐标轴交于点和点．

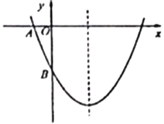
    （1）求该二次函数的解析式；

    （2）已知该函数图像的对称轴上存在一点，使得的周长最小．请求出点的坐标；

    （3）在（2）的条件下，在轴上找一点，使得是等腰三角形，请直接写出所有符合条件的点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．

    （1）求y关于x的函数关系式；（不需要写定义域）

    （2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）（问题发现）如图1，△ABC和△ADE均为等边三角形，点B，D，E在同一条直线上．填空：①线段BD，CE之间的数量关系为 ；②∠BEC = °．

    　　　　　　　　

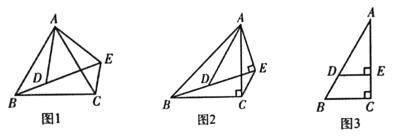
    （2）（类比探究）如图2，△ABC和△ADE均为等腰直角三角形，∠ACB=∠AED=90°，AC=BC，AE=DE，点B，D，E在同一条直线上，请判断线段BD，CE之间的数量关系及∠BEC的度数，并给出证明．

    （3）如图3，在△ABC中，∠ACB=90°，∠A=30°，AB = 5，点D在AB 边上，DE⊥AC于点E，AE = 3，将△ADE绕点A旋转，当DE所在直线经过点B时，CE的长是多少？（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AC＝BC，∠ACB＝α，点D为直线BC上一动点，过点D作DF∥AC交直线AB于点F，将AD绕点D顺时针旋转α得到ED，ED交直线AB于点O，连接BE．

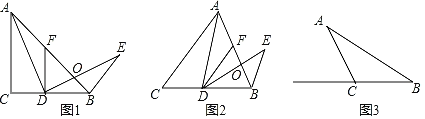
    （1）问题发现：

    如图1，α＝90°，点D在边BC上，猜想：

    ①AF与BE的数量关系是　 　；

    ②∠ABE＝　 度．

    （2）拓展探究：

    如图2，0°＜α＜90°，点D在边BC上，请判断AF与BE的数量关系及∠ABE的度数，并给予证明．

    （3）解决问题

    如图3，90°＜α＜180°，点D在射线BC上，且BD＝3CD，若AB＝8，请直接写出BE的长．

    查看答案和解析>>

    同步练习册答案