
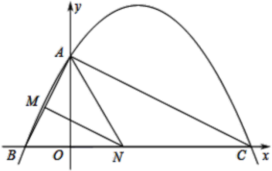
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0)、点C(8,0)两点,与y轴交于点A.
(1)求二次函数的表达式;
(2)连接AC、AB,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,线段AC上有一动点P,连接PM,求PM+![]() PC的值最小时,点P的坐标.
PC的值最小时,点P的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2) N(3,0); (3) P(1,
x+4;(2) N(3,0); (3) P(1,![]() ) .
) .
【解析】
(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)过点PD⊥x轴于点D,点E为M关于AC的对称点,作EF⊥x轴于点F,则PM+![]() PC的最小值即为EF的长.求出直线AC的解析式,并证明
PC的最小值即为EF的长.求出直线AC的解析式,并证明![]() ,再由(2)知
,再由(2)知![]() ,利用中点公式可得E的坐标,再将点E的横坐标代入直线AC,从而得解.
,利用中点公式可得E的坐标,再将点E的横坐标代入直线AC,从而得解.
(1)将点B,点C的坐标分别代入y=ax2+bx+4可得,
![]()
解得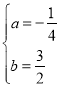 ,
,
∴二次函数的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设点N的坐标为(n,0)(﹣2<n<8),则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣![]() x2+
x2+![]() x+4中,令x=0,可解得y=4,
x+4中,令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=![]() BNOA=
BNOA=![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴![]()
∴![]()
∴![]()
∵﹣![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)如图,过点PD⊥x轴于点D,点E为M关于AC的对称点,作EF⊥x轴于点F,
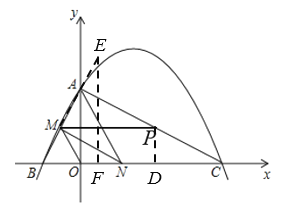
![]() ,易得
,易得![]() ,当E、P、D三点共线时,可知PM+
,当E、P、D三点共线时,可知PM+![]() PC的最小值即为EF的长.
PC的最小值即为EF的长.
由(2)可得M(-1,2),
由A(0,4),B(-2,0),C(8,0),得直线AC: ![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
即![]() 是直角三角形,且
是直角三角形,且![]() ,
,
∵M,E关于AC对称,
∴A(0,4)是ME的中点,由中点坐标公式得![]() ,
,
∴点P横坐标是1,代入![]() ,得y=
,得y=![]() ,
,
则P(1,![]() ) .
) .


科目:初中数学 来源: 题型:
【题目】 如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为( )
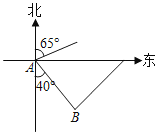
A.北偏西40°B.北偏东40°C.北偏西35°D.北偏东35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,培养学生自主、团结协作能力,某校推出了以下四个项目供学生选择:A.家乡导游:B.艺术畅游:C.体育世界:D.博物旅行.学校规定:每个学生都必须报名且只能选择其中一个项目,学校对某班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图,请结合统计图中的信息,解答下列问题:
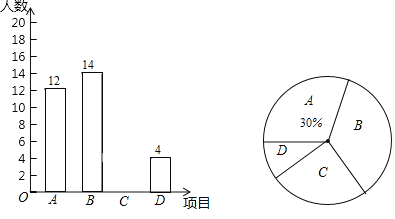
(1)求该班学生总人数;
(2)计算B项目所在扇形的圆心角的度数;
(3)将条形统计图补充完整;
(4)该校有1200名学生,请你估计选择“博物旅行”项目学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出随机摸球所有可能的结果;
(2)分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个电子团队维护一批电脑,维护电脑的台数y(台)与维护需要的工作时间x(h)(0≤x≤6)之间关系如图所示,请依据图象提供的信息解答下列问题:
(1)求乙队维护电脑的台数y(台)关于维护的时间x(h)的关系式;
(2)当x为多少时,甲、乙两队维护的电脑台数一样.
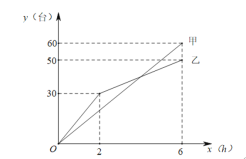
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行汉字听写大赛,学习对参赛者获奖情况进行统计,根据比赛成绩列出统计表,并绘制了扇形统计图
(1)参加此次比赛的学生共______________人.
(2)![]()
(3)若从一等奖中随机抽取两名学生,参加市级汉字听写大赛,请用树状图或列表的方法,求出所选的两名学生正好为一男一女的概率.
等次 | 男生 | 女生 |
一等奖 | 3 | m |
二等奖 | 6 | 12 |
三等奖 | 8 | 9 |
鼓励奖 | 6 | n |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com