
����Ŀ��Ϊ�˴����л����㴫ͳ�Ļ�������ѧ���������Ž�Э��������ijУ�Ƴ��������ĸ���Ŀ��ѧ��ѡ��A�����絼�Σ�B���������Σ�C���������磺D���������У�ѧУ�涨��ÿ��ѧ�������뱨����ֻ��ѡ������һ����Ŀ��ѧУ��ij��ѧ��ѡ�����Ŀ���������ͳ�ƣ�������������������������ͳ��ͼ������ͳ��ͼ�е���Ϣ������������⣺
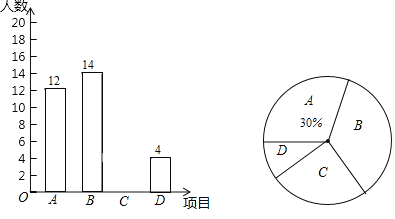
(1)��ð�ѧ����������
(2)����B��Ŀ�������ε�Բ�ĽǵĶ�����
(3)������ͳ��ͼ����������
(4)��У��1200��ѧ�����������ѡ�������С���Ŀѧ����������
���𰸡���1��40����2��![]() ����3������������4��120�ˣ�
����3������������4��120�ˣ�
��������
��1������A��Ŀ��Ƶ����������ռ�İٷֱȵõ��������������
��2����360������B��Ŀ��ռ�İٷֱȼ������B��Ŀ�������ε�Բ�ĽǵĶ�����
��3������������ȥ������Ŀ���������C��Ŀ��������Ȼ��ȫ����ͳ��ͼ��
��4�������������Բ���������ռ�İٷֱȼ��ɵõ��𰸣�
�⣺��1��������������У�12��30%=40���ˣ���
�ʴ�Ϊ��40��
��2��B��Ŀ�������ε�Բ�ĽǵĶ�����![]() ��
��
��3��C��Ŀ������Ϊ��40-12-14-4=10���ˣ���
������ͳ��ͼ���£�
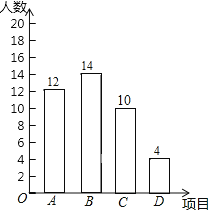
��4��![]() �ˣ�
�ˣ�
����ѡ�������С���Ŀѧ��������Ϊ1200�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
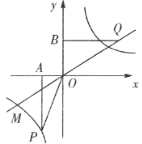
����Ŀ����ͼ����֪�����������ͷ�����������ͼ������![]() ����
����![]() Ϊ˫�����ϵ�һ�㣬
Ϊ˫�����ϵ�һ�㣬![]() Ϊ����ƽ����һ���㣬
Ϊ����ƽ����һ���㣬![]() ��ֱ��
��ֱ��![]() �ᣬ
�ᣬ![]() ��ֱ��
��ֱ��![]() �ᣬ����ֱ���
�ᣬ����ֱ���![]() ��
��![]() .
.
��1��д�������������ͷ����������Ĺ�ϵʽ.
��2������![]() ��ֱ��
��ֱ��![]() ���˶�ʱ��ֱ��
���˶�ʱ��ֱ��![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() �������ȣ�������ڣ������������ꣻ��������ڣ���˵������.
�������ȣ�������ڣ������������ꣻ��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� Ϊ������������������Ҫ�����������ɹ�������������������ṩ�������������죬������˾��![]() �����ͺŵĽ������ɹ�ѡ��.
�����ͺŵĽ������ɹ�ѡ��.
��1�����ɹ�˾2015��ÿ��![]() �����������ۼ�Ϊ
�����������ۼ�Ϊ![]() ��Ԫ�����������������ۣ�2017��ÿ���ۼ�Ϊ
��Ԫ�����������������ۣ�2017��ÿ���ۼ�Ϊ![]() ��Ԫ����ÿ��
��Ԫ����ÿ��![]() �ͽ�������ƽ���½���
�ͽ�������ƽ���½���![]() ��
��
��2��2017�������������б꣬���������ɹ�����װ���ɹ�˾![]() �����ͺŵĽ���������
�����ͺŵĽ���������![]() �����ɹ�ר����ܼƲ�����
�����ɹ�ר����ܼƲ�����![]() ��Ԫ���ɹ���ͬ�涨��ÿ��
��Ԫ���ɹ���ͬ�涨��ÿ��![]() ���������ۼ�Ϊ
���������ۼ�Ϊ![]() ��Ԫ��ÿ��
��Ԫ��ÿ��![]() ���������ۼ���
���������ۼ���![]() ��Ԫ.
��Ԫ.
��![]() �ͽ���������ɹ�������ף�
�ͽ���������ɹ�������ף�
����װ��ɺ���ÿ��![]() �ͺ�
�ͺ�![]() ��������һ��������ѷֱ��ǹ���۵�
��������һ��������ѷֱ��ǹ���۵�![]() ��
��![]() .�������ƻ�֧��
.�������ƻ�֧��![]() ��Ԫ��������.�ʸ��ƻ�֧���ܷ�����һ���������Ҫ��
��Ԫ��������.�ʸ��ƻ�֧���ܷ�����һ���������Ҫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����A=30����ֱ��a��b������C��ֱ��b�ϣ�ֱ��a��AB�ڵ�D����AC�ڵ�E������1=145��������2�Ķ�����( )

A.30��B.35��C.40��D.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�С����һ�λ�У���һ����ѧ�������������о���
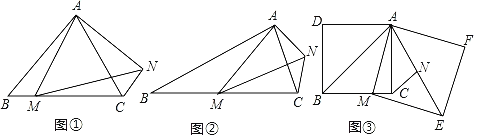
�����ⷢ�֣���1����ͼ�٣��ڵȱ�������ABC�У���M��BC��������һ�㣬����AM����AMΪ�����ȱ�������AMN������CN�����ABC�͡�ACN��������ϵΪ�� ����
����ʽ̽������2����ͼ�ڣ��ڵ���������ABC�У�AB��BC����M��BC��������һ�㣨�����˵�B��C������AM����AMΪ��������������AMN��ʹ��AMN����ABC��AM��MN������CN����̽����ABC���ACN��������ϵ����˵�����ɣ�
��������⣩��3����ͼ�ۣ���������ADBC�У���MΪBC����һ�㣬��AMΪ����������AMEF����NΪ������AMEF�����ģ�����CN��AB��AE����������ADBC�ı߳�Ϊ8��CN��![]() ��ֱ��д��������AMEF�ı߳���
��ֱ��д��������AMEF�ı߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
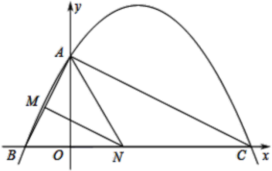
����Ŀ����ͼ����֪���κ���y��ax2��bx��4��ͼ����x�ύ�ڵ�B(��2��0)����C(8��0)���㣬��y�ύ�ڵ�A��
(1)����κ����ı���ʽ��
(2)����AC��AB������N���߶�BC���˶�(�����B��C�غ�)������N��NM��AC����AB�ڵ�M������AMN������ʱ����N������ꣻ
(3)����OM����(2)�Ľ����£��߶�AC����һ����P������PM����PM��![]() PC��ֵ��Сʱ����P�����꣮
PC��ֵ��Сʱ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵȱ������Σ���DΪƽ����һ�㣬����DB��DC����BDC��120�㣮
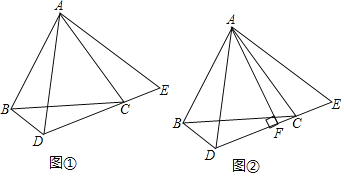
��1����ͼ��������D��BC�·�ʱ������AD���ӳ�DC����E��ʹCE��BD������AE��
����֤����ABD�ա�ACE��
����ͼ��������A��AF��DE�ڵ�F��ֱ��д���߶�AF��BD��DC���������ϵ��
��2����AB��2![]() ��DC��6��ֱ��д����A��ֱ��BD�ľ��룮
��DC��6��ֱ��д����A��ֱ��BD�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ij����ʻ�����У������е�ʣ������y����������ʻ·��x��ǧ�ף�֮����һ�κ�����ϵ���䲿��ͼ����ͼ��ʾ��
��1����y����x�ĺ�����ϵʽ��������Ҫд������
��2����֪�������е�ʣ������Ϊ8��ʱ���������Ὺʼ��ʾ���ͣ��ڴ˴���ʻ�����У���ʻ��500ǧ��ʱ��˾��������ǰ������ļ���վ��30ǧ��·�̣��ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·���Ƕ���ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��x2+2bx+1��2b(bΪ����)��
��1������(2��5)�ڸ��������ϣ���b��ֵ��
��2�����������ߵĶ���������(m��n)����n����m�ĺ�������ʽ��
��3������������x�ύ��֮��ľ������4����b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com