
【题目】如图,已知正比例函数和反比例函数的图像都经过点![]() ,且
,且![]() 为双曲线上的一点,
为双曲线上的一点,![]() 为坐标平面上一动点,
为坐标平面上一动点,![]() 垂直于
垂直于![]() 轴,
轴,![]() 垂直于
垂直于![]() 轴,垂足分别是
轴,垂足分别是![]() 、
、![]() .
.
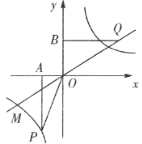
(1)写出正比例函数和反比例函数的关系式.
(2)当点![]() 在直线
在直线![]() 上运动时,直线
上运动时,直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 与
与![]() 的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
【答案】(1)正比例函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ;
;
(2)在直线![]() 上存在这样的点
上存在这样的点![]() 或
或![]() ,使得
,使得![]() 与
与![]() 面积相等.
面积相等.
【解析】
(1)用待定系数法进行求解,即可得到正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,![]() x),使得△OBQ与△OAP面积相等,则B(0,
x),使得△OBQ与△OAP面积相等,则B(0,![]() x).根据三角形的面积公式列出关于x的方程,解方程即可.
x).根据三角形的面积公式列出关于x的方程,解方程即可.
(1)设反比例函数的解析式为![]() ,正比例函数的解析式为
,正比例函数的解析式为![]() .
.
∵正比例函数和反比例函数的图像都经过点![]() ,∴
,∴![]() ,
,![]() . ∴
. ∴![]() ,
,![]() .
.
∴正比例函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() .
.
(2)当点![]() 在直线
在直线![]() 上运动时,假设在直线
上运动时,假设在直线![]() 上存在这一的点
上存在这一的点![]() ,使得
,使得![]() 与
与![]() 面积相等,则
面积相等,则![]() .
.
∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() . 当
. 当![]() 时,
时,![]() .
.
故在直线![]() 上存在这样的点
上存在这样的点![]() 或
或![]() ,使得
,使得![]() 与
与![]() 面积相等.
面积相等.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
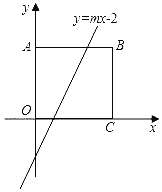
【题目】如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4).
(1)直线y=mx﹣2恰好把正方形ABCO的面积分成相等的两部分,则m=_____;
(2)若直线y=mx﹣2与正方形ABCO的边有两个公共点,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
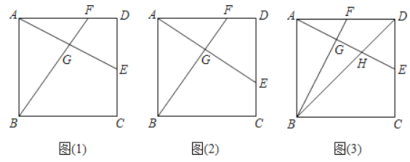
【题目】如图,正方形![]() 的边长为
的边长为![]() 分别是边
分别是边![]() 上的动点,
上的动点,![]() 和
和![]() 交于点
交于点![]() .
.
![]() 如图(1),若
如图(1),若![]() 为边
为边![]() 的中点,
的中点,![]() , 求
, 求![]() 的长;
的长;
![]() 如图(2),若点
如图(2),若点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,点
运动,点![]() 在
在![]() .上从
.上从![]() 向
向![]() 运动.两点同时出发,同时到达各自终点,求在运动过程中,点
运动.两点同时出发,同时到达各自终点,求在运动过程中,点![]() 运动的路径长:
运动的路径长:
![]() 如图(3), 若
如图(3), 若![]() 分别是边
分别是边![]() 上的中点,
上的中点,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的正切值.
的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
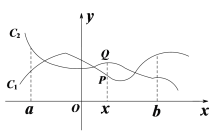
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,并说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
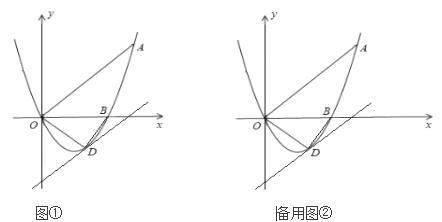
【题目】如图,已知抛物线 ![]() (
(![]() 为常数)经过点
为常数)经过点 ![]() ,与
,与 ![]() 轴相 交于点
轴相 交于点 ![]() 、
、![]() (点
(点 ![]() 在点
在点 ![]() 的右侧).
的右侧).
(1)求抛物线的解析式和点 ![]() 的坐标;
的坐标;
(2)将直线 ![]() 向下平移
向下平移 ![]() (
( ![]() )个单位长度后,得到的直线与抛物线只有一个公共点
)个单位长度后,得到的直线与抛物线只有一个公共点 ![]() ,求点
,求点 ![]() 的坐标;
的坐标;
(3)在(2)的条件下,连接 ![]() 、
、![]() ,在
,在 ![]() 正半轴上是否存在点
正半轴上是否存在点 ![]() ,使以
,使以 ![]() 、
、![]() 、
、 ![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.若存在,请求出点
相似.若存在,请求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为( )
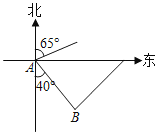
A.北偏西40°B.北偏东40°C.北偏西35°D.北偏东35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
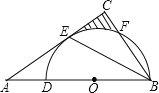
【题目】如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知∠A=30°,⊙O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,培养学生自主、团结协作能力,某校推出了以下四个项目供学生选择:A.家乡导游:B.艺术畅游:C.体育世界:D.博物旅行.学校规定:每个学生都必须报名且只能选择其中一个项目,学校对某班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图,请结合统计图中的信息,解答下列问题:
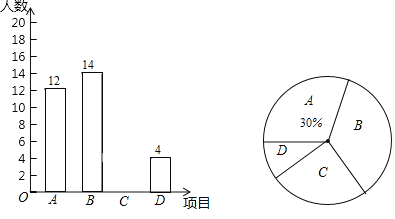
(1)求该班学生总人数;
(2)计算B项目所在扇形的圆心角的度数;
(3)将条形统计图补充完整;
(4)该校有1200名学生,请你估计选择“博物旅行”项目学生的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com